Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
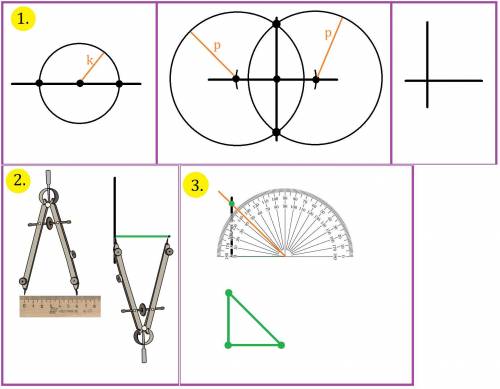
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.

Диагональ прямоугольника-это гипотенуза прям. треугольника, с катетом 30, второй катет-длина прямоугольника, назовем его х
по теореме Пифагора х=√50²-30²=√2500-900=√1600=40-длина,
30-ширина (по условию) Sпрям=40*30=1200-это площадь прямоугольника