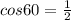
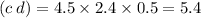
Sполн = 50+100√7 см².
Объяснение:
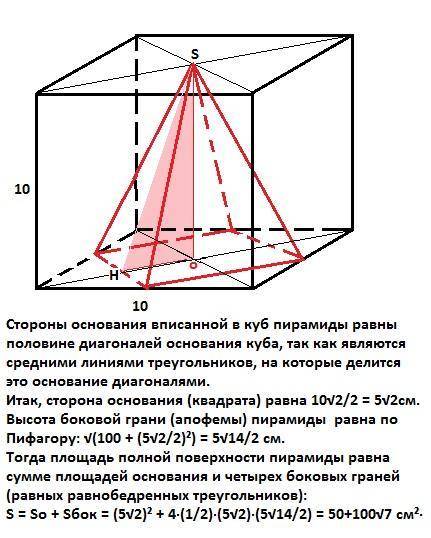
Стороны основания вписанной в куб пирамиды равны половине диагоналей основания куба, так как являются средними линиями треугольников, на которые делится это основание диагоналями.
Итак, сторона основания (квадрата) равна 10√2/2 = 5√2 см.
Высота боковой грани (апофемы) пирамиды равна по Пифагору:
√(100 + (5√2/2)²) = 5√14/2 см.
Тогда площадь полной поверхности пирамиды равна сумме площадей основания и четырех боковых граней (равных равнобедренных треугольников):
S = So + Sбок = (5√2)² + 4·(1/2)·(5√2)·(5√14/2) = 50+100√7 см²·
Будем решать это задание через части.
1. 7 : 9.
Найдем сколько всего частей: 7 + 9 = 16 частей.
Теперь узнаем сколько из 52 приходить на одну часть, для этого сделаем следующие действия:
52 : 16 = 3,25.
Теперь найдем сколько приходиться на 7 частей:
7 * 3,25 = 22,75.
Теперь найдем сколько приходиться на 9 частей:
9 * 3,25 = 29,25.
ответ: 7 : 9 = 22,75 : 29,25.
2. 2 : 9.
Найдем сколько всего частей: 2 + 9 = 11 частей.
теперь узнаем сколько из 52 приходить на одну часть:
52 : 11 = 4,727272.
Теперь найдем сколько приходиться на 2 части:
2 * 4,727272 = 9,454545.
Теперь найдем сколько приходиться на 9 частей:
9 * 4,727272 = 42,545448.
ответ: 2 : 9 = 9,454545 : 42,545448