Объяснение:
Дано:
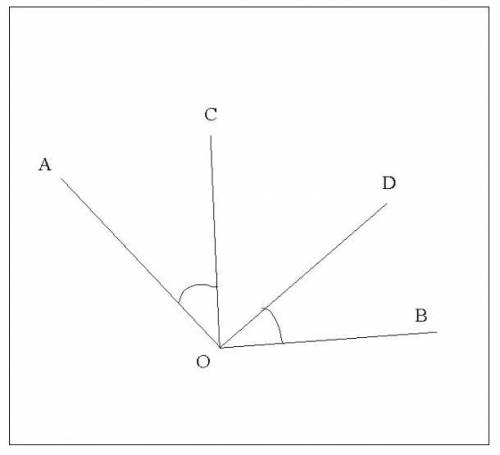
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
1. 4х+х=150
5х=150
х=30
ответ. 30°
2. х+х+2х=180
4х=180
х=45
ответ. 45°
3. 2х+3х=90
5х=90
х=18
3х-2х=х - разность.
ответ. 18°
4. Находим углы.
х+2х+3х=180
6х=180
х=30
30°,60°,90°.
Следовательно, данный треугольник - прямоугольный.
Меньшая сторона лежит против угла 30° и равна половине гипотенузы (гипотенуза, как большая сторона равна 8 см). Меньшая сторона равна 4 см.
Медиана, проведенная к гипотенузе, равна ее половине, т.е. 4 см.
Меньшая сторона + медиана, провед. к гипотенузе = 4+4 = 8 (см)
ответ. 8 см.
5. Так как треугольник равнобедренный, то высота, проведенная к основе (в данной задаче - это гипотенуза), является и медианой. А медиана, проведенная к гипотенузе, равна ее половине. Значит, гипотенуза равна двум медианам.
6·2=12 (см)
ответ. 12 см.