Question

Сфера задана уравнением x2+(y+3)2+(z-2)2=25 a) назовите координаты центра и радиус сферы б)определите,принадлежат ли данной сфере точки а и в ,если а(4; -3; -1),в(0; 1; 3)

Answer 1

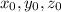Уравнение сферы: $(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$, где $x_0,y_0,z_0$ - координаты центра сферы, $R$ - радиус сферы.

Представим уравнение, данное в задаче, в общем виде.

$x^2+(y+3)^2+(z-2)^2=25\\\\(x-0)^2+(y-(-3))^2+(z-2)^2=5^2$

а) Отсюда координаты центра сферы О(0; -3; 2), радиус сферы R=5.

б) Подставим координаты точек А и В в исходное уравнение сферы. Если равенство будет выполняться, то точка принадлежит сфере.

А(4;-3;-1)

$4^2+(-3+3)^2+(-1-2)^2=25\\16+0+9=25\\25=25$

Равенство верно, значит точка А принадлежит данной сфере.

В(0;1;3)

$0^2+(1+3)^2+(3-2)^2=25\\0+16+1=25\\17\neq 25$

Равенство неверно, следовательно, точка В не принадлежит данной сфере.