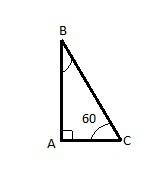
Построим прямоугольный треугольник АВС (угол А= 90 градусов, угол С=60 градусов).
Сумма углов треугольника равна 180 градусам. Зная это найдем угол В:
В=180-(А+С)=180-(90+60)=30 градусов.
Так как против меньшей стороны треугольника лежит меньший угол то меньшим катетом треугольника АВС будет сторона АС (В<С<А)
Катет, лежащий против угла 30 градусов равен половине гипотенузы.
Пусть катет АС=х см. Тогда гипотенуза ВС=2х см. Получаем уравнение:
х+2х=21
3х=21
х=21/3
х=7
Катет АС=7 см.
Гипотенуза ВС=2*7=14 см.
Тело вращения представляет из себя два конуса, приложенных основаниями. Высота конусов - половина стороны а/2, радиус основания - высота треугольника а√3/2, образующая равна а.
V= 2* 1/3* pi *R²*H= 2 * 1/3 * (a√3/2)²*a/2 = a³/4*pi.
S= 2 *pi*R*L = 2*pi*a√3/2*a= pi*a²*√3.