Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.
- - -
Дано :
ΔАВС - правильный (равносторонний).
АВ = √3.
АМ, ВН, СК - биссектрисы.
АМ ∩ ВН ∩ СК = L.
Найти :
Р(ΔALH) = ?
АВ = ВС = АС = √3 (по определению равностороннего треугольника).
В правильном треугольнике все его биссектрисы являются медианами и высотами.Соответственно, по определению медианы треугольника -
АН = НС = 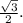
Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).
В равностороннем треугольнике все углы равны по 60°.То есть ∠А = 60°.
По определению биссектрисы треугольника -
∠ВАМ = ∠МАС = 60°/2 = 30°.
По определению косинуса острого угла прямоугольного треугольника -
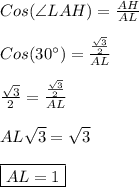
Отсюда -
LH = 0,5*AL = 1*0,5 = 0,5.
Периметр - это сумма длин всех сторон.Отсюда -
Р(ΔALH) = LH + AL + AH = 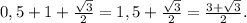
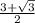 (ед).
(ед).