Данные точки лежат на поверхности шара, следовательно, не лежат на одной прямой.
Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость. Относительно к шару эта плоскость будет сечением, а сечение шара - круг.
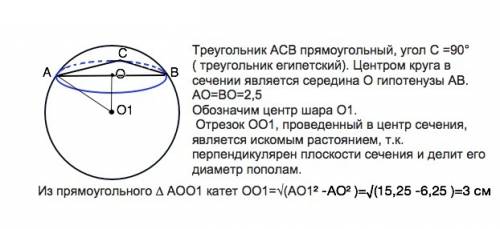
Соединив данные точки, получим треугольник АСВ, причем угол С =90° ( треугольник египетский). Тогда центром круга в сечении является середина О гипотенузы АВ.
r=АО=ВО=2,5
Обозначим центр шара О1.
Отрезок, проведенный в центр сечения, является искомым расстоянием, т.к. перпендикулярен плоскости сечения и делит его диаметр пополам.
Из прямоугольного ∆ АОО1 катет
ОО1=√(AО1² -АО² )=√(15,25 -6,25 )=√9=3 см
A1. Две прямые на плоскости называются параллельными, если они:
4) не пересекаются
А2. Один из признаков параллельности двух прямых гласит:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А3. Выберите утверждение, являющееся аксиомой параллельных прямых:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
А4. Если две параллельные прямые пересечены секущей, то:
Соответственные углы равны
А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:
Она перпендикулярна и другой
А6. Всякая теорема состоит из нескольких частей:
Условия и заключения
А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:
Накрест лежащие, соответственные, односторонние
А8. Аксиома – это:
Положение геометрии, не требующее доказательства
А9. Выберите утверждение, которое является признаком параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
А10. Если прямая не пересекает одну из двух параллельных прямых, то:
Другую прямую она тоже не пересекает
или
С другой прямой она совпадает