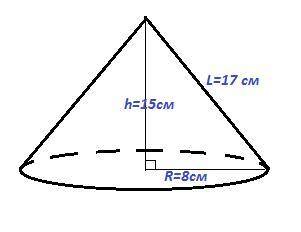
Площадь полной поверхности конуса равна 200π см, а его образующая - 17 см. Найдите объём конуса.
Полная поверхность конуса состоит из площади боковой поверхности и площади основания.
S = Sб + S₀ = πRL + πR² , где R - радиус основания, L - образующая
200π = πR · 17 + πR² | : π
R² + 17R - 200 = 0
D = 17² + 4 · 200 = 1089 = 33²
R₁ = (-17 + 33) : 2 = 8 см
R₂ = (-17 - 33) : 2 = -25 - не подходит по условию
Высота h, радиус основания R и образующая конуса L - это прямоугольный треугольник. Теорема Пифагора
h² = L² - R² = 17² - 8² = (17 - 8)(17 + 8) = 9·25
h = √(9·25) = 3·5 = 15 см
Объём конуса
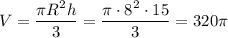 см³
см³
ответ: 320π см³
1) Сумма разных углов равна 180°, например, ∠1+∠2=180°,так как они будут смежными. Но в нашем случае сумма равна 78° , значмт это сума вертикальных углов, например, ∠2=∠4. Каждый из них равен половине данной сумме 78/2=39°.
∠1=∠3=∠5=∠7=39°.
Смежные им углы будут равны 180°-39°=141°.
∠2,=∠4,=∠6=∠8=141°.
2) По условию ∠2-∠1=16°. Пусть ∠1=х°, ∠2=(х+16)°,
Сумма смежных углов равна 180°,
х+х+16=180,
2х=180-16,
2х=164,
х=164/2=82°, ∠1=16°.
∠2=82+16=98°.
ответ: 82°, 98°.