Рисуем прямоугольный треугольник ABC.
Называем его с угла равным 90 градусам, тоесть угол A будет равен 90 градусам и верхний угол B а нижний правый C.
Из угла A проводим высоту к стороне BC.
У нас получается два треугольника ABH и AHC.
Пусть CAH будет равен 50 градусам (по условию).
Значит из 90* - 50* = 40* - угол BAH.
AH - высота
Угол BAH = 40*, следовательно
Угол B равен B=180*-(40*+90*) = 50*
Рассмотрим: треугольник ABC-прямоугольный.
Угол A=90*
Угол B=50*, то угол C=180*-(90*+50*)=40*
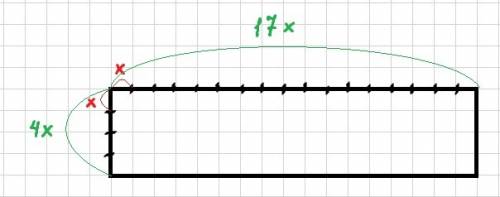
Отношение 4:17 означает, что 4 равных части одной стороны относятся к 17 таким же равным частям другой стороны.
Обозначим одну такую часть через х (смотри рисунок).
Тогда длина одной стороны будет 4х.
Длина второй стороны (смежной) будет 17х.
Площадь прямоугольника - произведение двух смежных сторон. Она известна: 272. Составим уравнение и найдем х, т.е. длину одной части.
4х*17х=272
68х²=272
х²=272:68
х²=4
х=√4
х=2
Длина одной части равна 2.
Значит длина одной стороны: 4х=4*2 = 8.
Длина второй стороны: 17х=17*2=34.
Периметр прямоугольника - сумма длин всех сторон.
Р= 8+8+34+34 = 84
ответ: 84.
cos 60= 1\2
tg 45= 1
ctg30 = корень 3\3