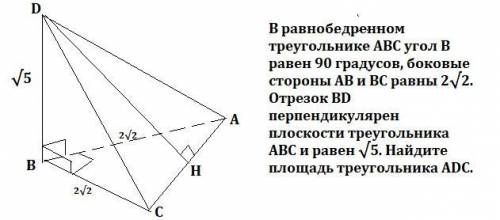
В равнобедренном Δ ABC угол B равен 90 градусов, боковые стороны AB и BC равны 2√2. Отрезок BD перпендикулярен плоскости треугольника АВС и равен √5.Найдите площадь ΔADC.
Объяснение:
Площадь треугольника ΔADC можно искать если знаешь либо стороны либо углы.
1)ΔАВС-прямоугольный, по т Пифагора АС=√((2√2)²+(2√2)² )=4.
2) ΔBDC=ΔBDA как прямоугольные по 2 катетам ⇒
DC=DA =√((√5)²+(2√2)²)=√13 ⇒ΔADC-равнобедренный .
3)Пусть DH⊥AC ,, тогда СН=2 .
ΔDCH -прямоугольный , по т. Пифагора DH=√( (√13)²-2²)=3
4) S(ADC)=1/2*AC*DH, S(ADC)=1/2*4*3= 6( ед²)
Треугольник равнобедреный,значит
АВ=ВС
ВК-медиана,значит она делит сторону пополам и
АК=КС
Медиана делит треугольник АВС на два равных треугольника
АВК=ВКС
Углы при основании треугольника АВС равны между собой,т е
Угол А равен углу С
ВК-общая сторона
Нам известно 3 стороны-это третий признак равенства треугольников-если три стороны одного треугольника равны трём сторонам другого треугольника равны между собой,то треугольники равны
Объяснение:
А можно и по первому признаку-две стороны и угол между ними АВ=ВС
АК=КС и угол А равен углу С
1.Т.к. угол СДЕ = 102град, треугольник СДЕ - равнобедренный => угол ДСЕ=углу ДЕС=(180-102):2=39град=> тк угол СНЕ = 90град(СН-высота)=> угол НСЕ=180-90-39=51градус