Решение.
1) Проведем луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно 5 равных отрезков АА1, А1А2, А2А3, А3А4, А4А5 т. е. столько
равных отрезков, на сколько равных частей нужно разделить данный отрезок А В.
2) Проведем прямую А5В и построим прямые, проходящие через точки А4, А3, А2, А1 и параллельные прямой А5В.
3) Эти прямые пересекают отрезок АВ в точках, которые по теореме Фалеса делят отрезок АВ на 5 равных частей.
д
Объяснение:
Дано: отрезок АВ.
Разделить отрезок на 5 равных частей.
Пусть AC=x, тогда в ΔABC по формуле Герона:
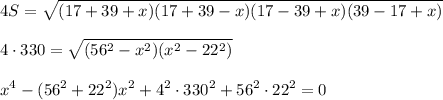
Решим квадратное уравнение относительно x².
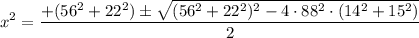
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
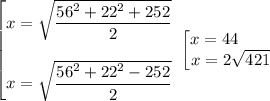
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
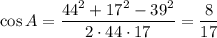
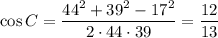
По формуле связи косинуса и тангенса:
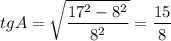
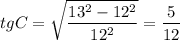
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
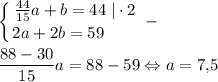
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
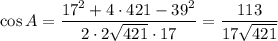
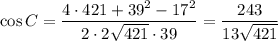
По формуле связи косинуса и тангенса:
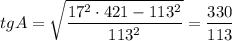
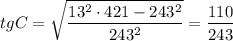
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
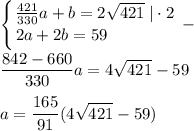
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=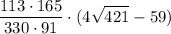 > 113/√421.
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.