3) Дано:
АВCD - ромб,
AC и BD - диагонали ромба,
О - точка пересечения диагоналей,
угол BCD = 104*
Найти углы ABO.
Решение: возьмем произвольный ромб и обозначим его как ABCD, проведем в нем диагонали AC и BD. Они пересекутся в точке О. Известно также, что диагонали ромба перпендикулярны и делят его углы пополам. Тогда угол ВСО = углу ОСD = 104/2=51*. Рассмотрим один из получившихся треугольников - ВОС. В нем угол ВОС = 90* (так как диагонали ромба перпендикулярны). Угол ВСО = 51*, угол ВОС = 90*, значит угол ОВС = 180 - (51*+90*) = 39*. Но треуг. ВСО = треуг. АВО и значит все стороны и углы одного соответственно равны сторонам и углам другого. То есть в треугольнике АВО угол АВО = 39*, а угол ВОА = 90*.
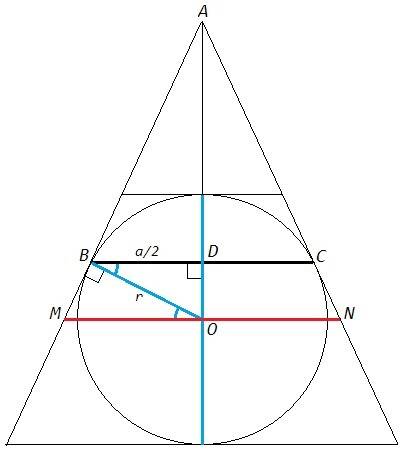
MN - средняя линия трапеции. Средняя линия проходит через центр вписанной окружности.
Отрезки касательных из одной точки равны, △BAC - равнобедренный. Параллельные линии отсекают от угла подобные треугольники. Средняя линия MN параллельна основаниям, основания параллельны BC, MN||BC => △MAN~△BAC, △MAN - равнобедренный. Центр вписанной окружности лежит на биссектрисе. Биссектриса в равнобедренном треугольнике является высотой и медианой, ∠BDO=90, BD=BC/2=a/2, MO=MN/2.
Радиус перпендикулярен касательной, ∠OBM=90.
Накрест лежащие углы при параллельных равны, ∠MOB=∠OBD.
△MOB~△OBD (по двум углам)
MO/OB=OB/BD <=> (MN/2)/r=r/(a/2) <=> MN=4r^2/a
В трапецию вписана окружность, h=2r.
S=MN*h =4r^2/a *2r =8r^3/a
7² = 3² + х²
х² = 7² - 3² = 49 - 9 = 40
х = √40 = 2√10 м
Зная высоту и длину стены, найдём её площадь:
S0 = 15 * 2√10 = 30√10 м²
Так как 20% площади красить не надо, остаётся всего 80%:
S = 0,8*S0 = 0,8 * 30√10 = 24√10 м² = 76 м² (приближённо)