1. Могут.
2. б) 6 см
3. б) 45°
Объяснение:
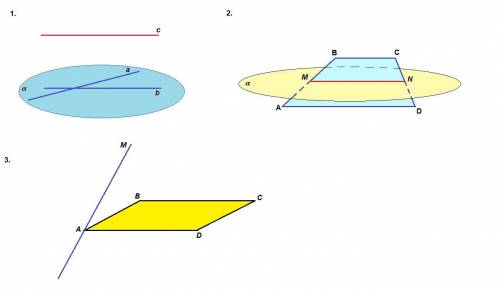
1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.
Прямые с и b могут быть параллельными.
2.
а) Так как точки М и N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.
MN - средняя линия трапеции, значит
AD║MN, ⇒ AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).
б) 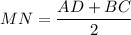
AD + BC = 2MN
BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см
3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.
а) ВС лежит в плоскости (АВС),
МА пересекает (АВС) в точке А,
А не лежит на прямой ВС, значит
МА и ВС скрещивающиеся.
б) ∠(МА, AD) = 45° по условию,
BC║AD, значит
∠(МА, ВС) = 45°
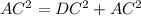
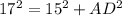
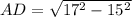
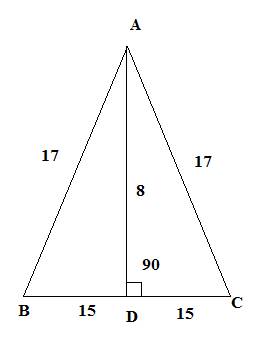
АВСД-прямоугольник
ВС=16 см
ВД-диагональ
ВД=20см
Найти:
SАВСД
Решение:
1.Рассмотрим треугольник ВСД,
Он прямоугольный, тк АВСД- прямоугольник.
По теореме Пифагора
ВС ( в квадрате) + СД (в квадрате) = ВД ( в квадрате)
256 + СД (в квадрате) = 400
СД ( в квадрате) = 400-256= 144
Значит СД=12 см
2. Рассмотрим прямоугольник АВСД
S прямоугольника= ав
SАВСД= 20*12= 320 см квадратных