ответ: 16√2
Объяснение:
Сумма углов трапеции, прилежащих к одной боковой стороне, равна 180°.
∠BCD + ∠CDA = 180°
∠CDA = 180° - ∠BCD = 180° - 150° = 30°
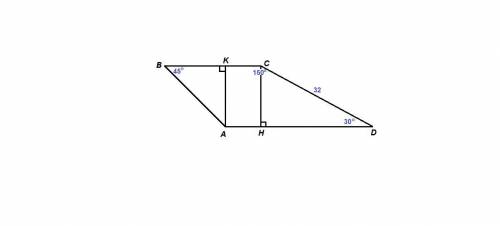
Проведем высоты СН и АК.
ΔCHD: ∠CHD = 90°,
СН = 1/2 CD = 1/2 · 32 = 16, по свойству катета, лежащего против угла в 30°.
АК = СН = 16 как высоты трапеции.
ΔАВК: ∠АКВ = 90°,
∠ВАК = 90° - ∠АВК = 45°, так как сумма острых углов прямоугольного треугольника равна 90°.
∠АВК = ∠ВАК = 45°, ⇒ ΔАВК равнобедренный, значит
ВК = АК = 16.
По теореме Пифагора:
АВ = √(АК² + ВК²) = √(16² + 16² ) = √(16² · 2) = 16√2
Найдите неизвестную сторону треугольника, если
АВ=3см, ВС=8см.
2. Найдите площадь треугольника АВС, если дано: АВ=5 см,
АС=14 см, угол А равен 60 градусов.
3. Найдите площадь параллелограмма с острым углом 30
градусов, если его стороны равны 24 см и 5 см.
4. Боковая сторона равнобедренного треугольника равна
18 м. Найдите площадь данного треугольника, если угол
между боковыми сторонами равен 120 градусов.
5. Даны точки А (1;4), В (3;7), С (5;2)
1)Найдите координаты векторов АВ и ВС.
2)Вычислите сколярное произведение векторов АВ и ВС.
6. Вычислите скалярное произведение двух векторов, если
их модули (длины) равны: 3 и 4, а угол между ними
равен: а) 60 градусов, в) 120 градусов.