Question

Дан квадрат abcd со стороной, равной 1, и проведена его диагональ bd, равная √2. чему равен косинус угла bda ?

Answer 1

Дан квадрат ABCD со стороной, равной 1, и проведена его диагональ BD, равная √2. Чему равен косинус угла BDA?

Косинус угла есть отношение прилежащего к нему катета на гипотенузу.

$\displaystyle cos(BDA)= \frac{AD}{BD}$

$\displaystyle cos(BDA)=\frac{1}{\sqrt{2} } \\\\cos(BDA)=\frac{1*\sqrt{2}}{\sqrt{2} *\sqrt{2}}\\\\cos(BDA)=\frac{\sqrt{2}}{2}$

ответ: √2/2

Answer 2

Дано :

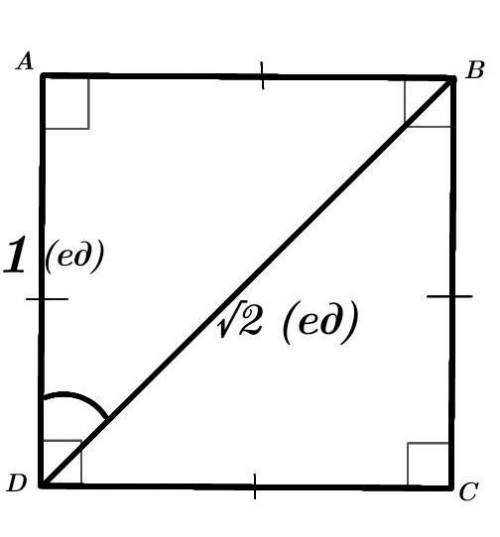
Четырёхугольник ABCD — квадрат.

AD = 1 (ед).

BD — диагональ = √2 (ед).

Найти :

соs(∠BDA) = ?

Квадрат — четырёхугольник, всё стороны которого равны, а все углы прямые.

Рассмотрим прямоугольный ∆ABD.

Косинус острого угла прямоугольного треугольника — отношение прилежащего катета к гипотенузе.

В нашем случае катет, прилежащий к ∠BDA — AD, а гипотенуза — BD (так как лежит против прямого угла).

То есть —

cos(∠BDA) = AD/BD

cos(∠BDA) = 1 (ед) / √2 (ед)

cos(∠BDA) = 1/√2

Или —

cos(∠BDA) = (√2)/2 (одно и тоже).

(√2)/2.