Відповідь:
АВ(10;5)
Пояснення:
АВ вектор, А-початок вектора
В- кінець вектора щоб знайти координати цілого вектору,треба відповідну координату по Х кінця(Вх) відняти координату початку (Ах) так само і по У АВ(4-(-6);5-0) АВ(10;5)
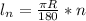 , где n - градусная мера соответственного центрального угла.
, где n - градусная мера соответственного центрального угла.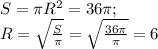 , где S - площадь круга.
, где S - площадь круга.
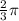 см.
см.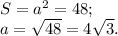
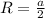 , где a - сторона квадрата.
, где a - сторона квадрата.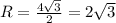
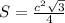 , где c - сторона правильного треугольника.
, где c - сторона правильного треугольника.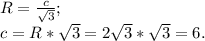
 .
.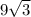 см.
см.
В равностороннем треугольнике все очень просто. Сначала находим ВЫСОТУ из точки В, она равна 13*корень(3)/2. По идее уже тут можно воспользоваться тем, что высота - одновременно и медиана, то есть найти её (высоту-медиану) из прямоугольного треугольника с гипотенузой 13 и одним из катетов 13/2. Второй катет (то есть высота-медиана) будет как раз 13*корень(3)/2 (теорема Пифагора :)).
А теперь вспоминаем, что точка О лежит на этой медиане-высоте на расстоянии 2/3 её длины, считая от вершины.
То есть ОВ = (13*корень(3)/2)*(2/3) = 13*корень(3)/3.
ответ:АВ(10;5)
Объяснение:
Координаты АВ находим за формулой:
АВ(х2-х1);(у2-у1),тоесть от координатов конца вектора "а" отнимаем начало вектора ",а" ,с вектором "В" аналогично
Подставляем:
АВ(4-(-6));(5-0)
АВ(10;5)