В равнобедренном тр-ке углы при основании равны.
Док-во:
1) Проведем к свнованию AC биссектрису BK => угол 1 = углу 2 пусть.
2) Рассмотрим тр-к ABK и тр-к CBK
1) AB=BC ( тр-к р/б )
2) угол 1 = углу 2 ( по условию )
3) BK = BK ( общая )
из этого всего следует, что тр-к ABK = тр-ку CBK по 1 признаку равенства тр-ков иди по двум сторонам и углу между ними => угол 1 равен углу 2, т.к это соответственные углы в равных тр-ках.
Писал по моему конспекту, так-что это не копипаст.
С линейки начертим остроугольный треугольник ABC, при этом AB < BC.В этом треугольнике есть высота H, как и в других.Теперь проведём ровную линию от точки B до H.Так же сказано, чтобы провести линию от медианы M до B.На рисунке показано где расположена медиана M.(M середина AC)
2.Сначала изобразим обычный отрезок a.Так же изобразим c, при этом c>a.
Нарисуем прямоугольный треугольник ABC.
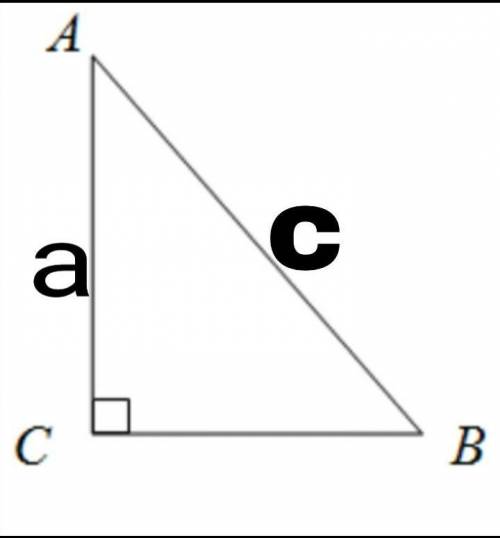
В задании сказано изобразить прямоуг. треуг. с катетом а и гипотинузой с.В таком треугольнике 2 катета и 1 гипотинуза.Катет a расположен между A и C.Разумеется длина катета равна длине отрезка а.
Гипотенуза с находится между A и B.
Разумеется длина гипотенузы равна длине отрезка с
ответ:всё на рисунках.
P.S. на 2 рис. я выделил a и c это отрезки которые вошли в треуг.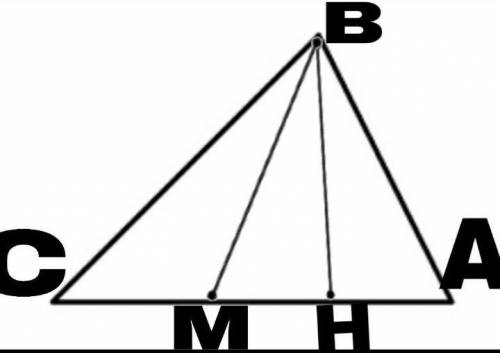
Угол СДМ=ЕДМ=37° (ДМ - биссектриса)
Треугольник ДNM - равнобедренный, углы при основании ДМ - равны
Угол ЕДМ=ДМN=37°
Сумма всех углов в треугольнике=180°
Угол DMN=180-2*37=180-74=106
ответ: 37°, 37°, 106°