Дано :
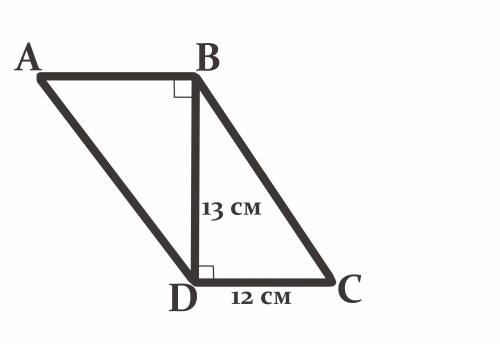
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
ответ:Если две прямые на плоскости,в данный момент это ВК и MN ,перпендикулярны к одной и той же прямой АС,то они параллельны,т к к прямой в плоскости из любой точки можно провести только один перпендикуляр
Параллельность прямых доказана
Теперь об углах
<СМN и <СВК являются соответственными и равны между собой
<СМN=<CBK=46 градусов
В условии сказано,что ВК биссектриса угла АВС
Биссектриса делит угол из которого она проведена на два равных угла,один из них угол СВК
<АВС=<СВК•2=46•2=92 градуса
Объяснение:
Из этого следует:
х+2х+4х+8х+16х=15500
31х=15500
х=500
ответ: в первый день он потратил 500 рублей