1)Пусть АВС-равнобедренный треугольник,АС-основание=12 см.
АВ=ВС=10 см
Проведем высоту ВН
Так как треугольник равнобедренный,то высота,проведенная к основанию,является и медианой,и биссектрисой.
Так как ВН-высота,то образуется прямоугольный треугольник АВН,причем из-за того,что ВН ещё и медиана,то АН=НС=12/2=6см.
Теперь по теореме Пифагора находим катет ВН
ВН=корень из(АВ^2-АН^2)
ВН=корень из(64)
ВН=8см
Sтреугольника АВС=(ВН*АС)/2
S=(8*12)/2
S=48 кв. см
ответ:48 кв.см.
2)параллелограмм ABCD
Проведём из угла В на AD высоту BK.
∆ABK-прямоугольный. ےА=30°
Следовательно BK=AB:2, как катет, лежащий против угла 30°
AB=12. Тогда BK=6; S=16×6=96 кв.см.
ответ:96 кв.см.
3)Дано:
АВСD-трапеция,
АВ=СD=13 см.
АD=20см
ВС=10см
Найти:S
Проводим высоту ВН,так как трапеция равнобедренная,то АН будет равен (20-10)/2=5 см
Образовался прямоугольный треугольник АВН,находим катет(высоту) ВН
ВН=корень из(АВ^2-AH^2)
ВН=корень из(169-25)
ВН=12 см.
S=((АD+ВС)/2)*ВН
S((20+10)/2)*12=180 кв.см.
ответ:180 кв.см
Подробнее - на -
Объяснение:
Объяснение:
Обозначим основание пирамиды АВСД, её вершину - М.
Все ребра пирамиды выходят из одной вершины и равны между собой, следовательно, проекции ребер равны.
Вокруг основания можно описать окружность ( прямоугольник).
Её центр- в точке пересечения диагоналей данного прямоугольника. Основанием О высоты МО будет этот центр.
Катеты ВС= 3 и АВ=4 указывают на то, что треугольник АВС - египетский и его гипотенуза АС=5. ( Можно проверить по т.Пифагора).
Тогда АО=2,5.
Высоту МО найдем по т.Пифагора:
МО²=АМ²-АО²
МО=√( 11²-2,5²)=√114,75
МО=√(25*9*51):√100=1,5√51
5
ответов осталось
Получи неограниченный доступ к миллионам подробных ответов
ОФОРМИ ПОДПИСКУ
Подробнее - на -
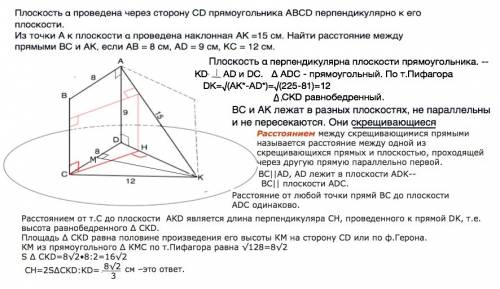
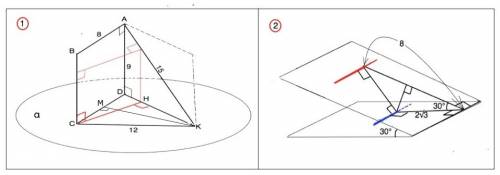
1) Плоскость α проведена через сторону CD прямоугольника АВСD перпендикулярно к его плоскости.
Из точки А к плоскости α проведена наклонная АК =15 см.
Найти расстояние между прямыми ВС и АК, если АВ = 8 см, AD = 9 см, КС = 12 см.
Сделаем рисунок.
Плоскость α перпендикулярна плоскости прямоугольника. ⇒
KD⊥AD и ⊥DC. ∆ АDC - прямоугольный. По т.Пифагора
DK=√(AK*-AD²)=√(225-81)=12
∆CKD равнобедренный.
ВС и АК лежат в разных плоскостях, не параллельны и не пересекаются. Они скрещивающиеся.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
ВС║AD, AD лежит в плоскости ADK⇒ ВС║плоскости ADC.
Расстояние от любой точки прямой ВС до плоскости ADC одинаково.
Расстоянием от т.С до плоскости является длина перпендикуляра СН, проведенного к прямой DK ( т.к. они лежат в одной плоскости), т.е. высота равнобедренного ∆ СКD.
Площадь ∆ СКD равна половине произведения его высоты КМ на сторону СD.
КМ из прямоугольного ∆ КМС по т.Пифагора равна √128=8√2
S ∆ CKD=8√2•8:2=16√2
CH=2S∆CKD:KD=(8√2)/3 см –это ответ.
–––––––––––––––––––––––––––––––
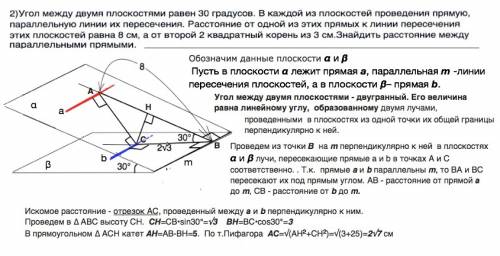
2) Обозначим данные плоскости α и β
Пусть в плоскости α лежит прямая а, параллельная m -линии пересечения плоскостей, а в плоскости β– прямая b.
Угол между двумя плоскостями - двугранный. Его величина равна линейному углу, образованному двумя лучами, проведенными в плоскостях из одной точки их общей границы перпендикулярно к ней.
Проведем из точки В на m перпендикулярно к ней в плоскостях α и β лучи, пересекающие прямые а и b в точках А и С соответственно. . Т.к. прямые a и b параллельны m, то BA и ВС пересекают их под прямым углом. АВ - расстояние от прямой а до m, СВ - расстояние от b до m.
Искомое расстояние - отрезок АС, проведенный между а и b перпендикулярно к ним.
Проведем в ∆ АВС высоту СН.
СН=СВ•sin30°=√3
ВН=ВС•cos30°=3
В прямоугольном ∆ АСН катет АН=АВ-ВН=5.
По т.Пифагора
АС=√(AH²+CH²)=√(3+25)=2√7 см