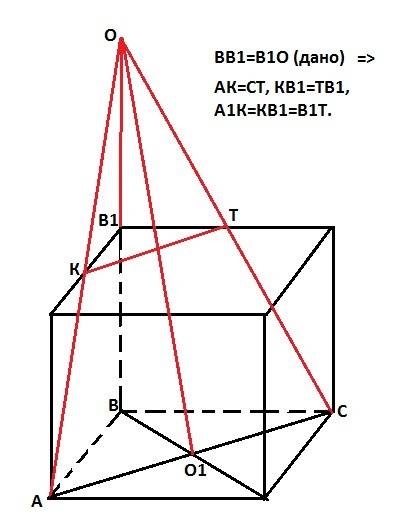
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.

/А биссектриссой поделили на два-/1,/2
ад-биссектриса,медиана и высота,т.к. авс-р/б(равнобедренный)=>
вд=вс,/1=/2,ад-общая=>авд=асд по 1 признаку,
значит ас=ав,следовательно авс-равносторонний,/а=,в=/с=180:3=60