Площадь треугольника равна половине произведения высоты на сторону, к которой проведена.
S=a•h:2
• Если высоты двух треугольников равны, то их площади относятся как основания.
Высота ∆ ADC и ∆ ABC общая.
Подробно.
S(ABD):S(ABC)=AD:AC
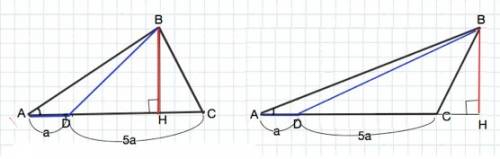
Точка D по условию делит АС в отношении 1:5.
Примем AD=a, тогда DC=5a.
AC=а+5а=6a
S(ABD):A(ABC)=1/6
S(ABC)=36
S(ABD)=36:6=6 см²
-----------
Площадь треугольника можно найти и по формуле
S=a•b•sinα:2, где a и b стороны треугольника, α - угол между ними.
Угол А общий для ∆ABD и ∆ABC, поэтому
S (ABD):S (ABC)=AB•AD:AB•AC, т.е. получается то же отношение AD:AC, равное для данного треугольника 1/6.
Коэффициент подобия:
k = 3/5
Отношение периметров подобных многоугольников равно коэффициенту подобия:
Р₁ : Р₂ = 3 : 5
Пусть х - одна часть, тогда Р₁ = 3х, Р₂ = 5х.
3x + 5x = 560
8x = 560
x = 70
P₁ = 70 · 3 = 210