Дано: треугольник kcm (1; 7); (-2; 4); (2; 0). найти: cos угла m

Question

Геометрия: Дано: треугольник kcm (1; 7); (-2; 4); (2; 0). найти: cos угла m

zahidamamirova · Accepted Answer

Дано: (рисунок)

Найти: AB

Решение: Опустим на сторону BC вершину AD, проходящую через точку A.

Так как вершина является перпендекуляром, то углы ADC и ADB равны 90⁰.

Так как сумма углов треугольника равна 180⁰, найдем углы CAD и DAB:

угол CAD=180⁰-30⁰-90⁰=60⁰

угол DAB=180⁰-90⁰-45⁰=45⁰

Из последнего выражения следует, что треугольник ADB - равнобедренный.

Найдем сторону AD треугольника CAD, пользуясь выражением «в прямоугольном треугольнике катед против 30⁰ равен половине гипотенузы»:

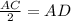
$\frac{AC}{2}=AD$

AD=6 см

Так как треугольник ADB равнобеднеррый, то AD=DB

Теперь, найдем сторону AB по теореме Пифагора:

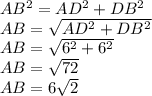
$AB^2=AD^2+DB^2\\ AB=\sqrt{AD^2+DB^2}\\ AB=\sqrt{6^2+6^2}\\ AB=\sqrt{72}\\ AB=6\sqrt{2}$