Объяснение:
1
180°-(50°+35°)=95°
2
180°-(65°+40°)=75°
3
(180°-80°):2=50°
4
180°-2*36°=108
5
х+х+20°=90°
2х=90°-20°
2х=70°
х=70°:2
х=35° - первый угол,
35°+20°=55° - второй угол.
6
х+2х=90°
3х=90°
х=90°:3
х=30° - первый угол,
30°*2=60° - второй угол.
7
3+5=8
Такого треугольника не существует.
8
1,3+1,8 > 3
Такой треугольник существует.
9
<A+<B+<C=180°
<A+<C=180°-<B=180°-110°=70°
<OAC+<OCA+<AOC=180°
<OAC+<OCA=1/2(<A+<C)
<AOC=180°- 1/2(<A+<C) =180°- 1/2*70°=145°
10
<A+<B+<C=180°
<B+<C=180°-<A=180°-106°=74°
<OCB+<OBC+<BOC=180°
<OCB+<OBC=1/2(<B+<C)
<BOC=180°- 1/2(<B+<C) =180°- 1/2*74°=143°
11
<2=90°-60°=30°
c=2a
a+2a=18
3a=18
a=18:3
a= 6 см
c=2*6=12 см
12
<2=90°-60°=30°
c=2a
a+2a=42
3a=42
a=42:3
a= 14 см
c=2*14=28 см
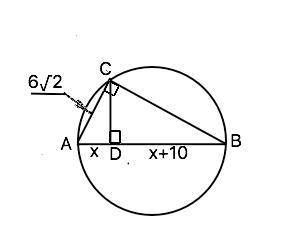
ответ: 9 см
Объяснение: Соединим С и В. Угол АСВ опирается на диаметр и равен половине градусной меры дуги АВ. Угол АСВ=90°.
Отрезок СD - высота ∆ АСВ, АD и ВD - проекции катетов на гипотенузу. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.⇒ АС=√(AD•AB). Примем АD=х, тогда ВD=х+10, а гипотенуза АВ=2х+10. ⇒ х•(2х+10)=72.
Выполнив необходимые действия и сократив все члены на 2, получим приведенное квадратное уравнение х²+5х-36=0 По т.Виета сумма корней приведённого квадратного трехчлена равна его второму коэффициенту с противоположным знаком, а произведение – свободному члену.
х₁+х₂=-5
х₁•х₂=36
-36=-9+4
-5= -9+4 ⇒ х=4, (отрицательный корень -9 не подходит).
Диаметр АВ=4+14=18 см, а радиус, соответственно, 18:2=9 см
* * *
Ясно, что задачу можно решить и через дискриминант. ответ будет тем же.
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
подставим заданные значения и выполним преобразования:
(х -2)/( -3 -2) = (у + 1)/(15 + 1)
16х - 32 = -5у - 5
у = ( -16/5) *х + 27/5