Высотой трапеции называют отрезок прямой, , заключенный между основаниями. и перпендикулярный им. Обычно это отрезок, проведенный из вершины угла при одном основании перпендикулярно к противоположному основанию.
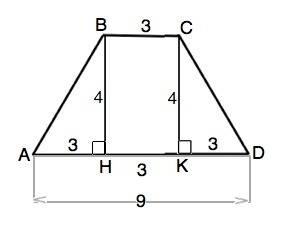
Высота РАВНОБЕДРЕННОЙ трапеции ABCD, проведенная из тупого угла, делит большее основани на отрезки, меньший из которых равен полуразности оснований (на рисунке приложения это АН ( или КD), а больший - их полусумме ( на рисунке это АК или DH).
АН=(АD-ВС):2=3
Из прямоугольного ∆ АВН по т. Пифагора
АВ=√(BH²+AH²)=√(16+9)=5
Трапеция равнобедренная. CD=AB=5
Периметром называется сумма длин всех сторон многоугольника.
P=AB+BC+CD+AD=5+3+5+9=22 см
углы
2*arcsin(3/4) и 2*arccos(3/4)
вторая диагональ
2*sqrt(24^2-(36/2)^2) = 12*sqrt(7);
площадь равна половине произведения диагоналей, а высота равна площади, деленной на основание, то есть сторону. В результате получается, что высота равна
9*sqrt(7)