Здесь главное сделать правильный чертеж, остальное уже просто.
Так как высота проведена к продолжению АD, она находится вне ромба.
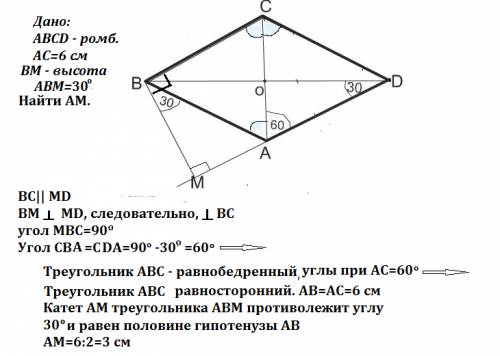
ВМ - высота, перпендикулярна МD.
ВС и АD параллельны как стороны параллелограмма, ⇒
ВМ перпендикулярна ВС, угол МВС=90º
Угол МВА=30ª, тогда угол СВА=90º-30º=60º. Т.к. стороны ромба равны, треугольник АВС - равнобедренный. Углы при основании АС=(180º-60º):2=60º⇒
ΔАВС - равносторонний.
Тогда АВ=АС=6 см.
В прямоугольном треугольнике АМВ углу МВА противолежит катет МА.
Катет, противолежащий углу 30º, равен половине гипотенузы.
АМ=АВ:2=3 см
Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
Ортоцентр — точка пересечения трёх высот треугольника. Во всяком треугольнике точка пересечения медиан, центр описанного круга и ортоцентр лежат на одной прямой.
Серединные перпендикуляры к сторонам треугольника (или другого описываемого окружностью многоугольника) пересекаются в одной точке — центре описанной окружности.
По теореме Пифагора:
АС² = АВ² + ВС² ⇒ АВ² = АС² - ВС² = 7 - 3 = 4(см)