Задача: Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус кола, описаного навколо цього трикутника, дорівнює 16 см.
Рішення:
Формула кола, вписаного в рівносторонній трикутник:
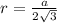 , де а — сторона правильного тр-ка
, де а — сторона правильного тр-ка
Знайдемо сторону а через формула кола, описаного навколо рівностороннього тр-ка:
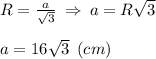
Підставимо значення у формулу кола, вписаного в рівносторонній тр-к

Відповідь: Радіус кола, вписаного в рівносторонній трикутник, рівний 8 см.
Задача: Точка перетину висот BK і PH трикутника BEP є центром вписаного в нього кола. Доведіть, що тр-к BEP рівносторонній.
Рішення:
Центром вписаного в коло трикутника є перетин бісектриса тр-ка, отже і BK та PH є бісектрисами. Висота є бісектрисою, якщо суміжні сторони рівні.
BK — висота/бісектриса ⇒ PB = EB;
PH — висота/бісектриса ⇒ PB = EP.
Відповідно, PB = EB = EP ⇒ ΔBEP — рівносторонній, що і потрібно було довести.
1) Угол СОА=ВОМ (как вертикальные)
2) Угол АСО=ВМО (как накрест лежащие при секущей СМ и параллельных прямых СА и ВМ)
3) Угол САО=ОВМ (как накрест лежащие при секущей ВА и параллельных прямых СА и ВМ )
Следовательно, треугольники СОА И ВОМ-подобные
Теперь можем составить пропорцию и найти сторону ОМ отношению СА:ВМ=СО:ОМ, отсюда ОМ=ВМ*СО/СА=3*12/18=2, из этого СМ=2+12=14 смответ: СМ=14 см