если половинки диагоналей обозначить a и b, то сторона ромба будет
sqrt(a^2+b^2);
Площадь ромба равна половине произведения диагоналей, то есть 2*a*b =120;
По условию, раз а и b - половинки диагоналей, то a - b = 7;
(a-b)^2 = 49;
a^2+b^2 - 2*a*b = 49;
a^2+b^2 = 49+120 = 169 = 13^2;
Поэтому сторона ромба равна 13, периметр 52
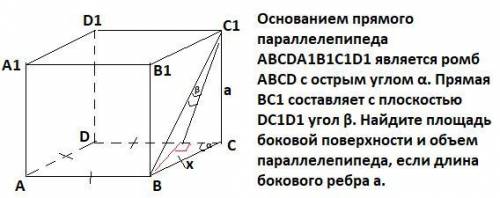
Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб АВСD с острым углом α. Прямая BC1 составляет с плоскостью DC1D1 угол β. Найдите площадь боковой поверхности и объем параллелепипеда, если длина бокового ребра а.
Объяснение:
S(бок)=Р*L, V=S(осн.)*L ,где L-боковое ребро , перпендикулярное плоскости основания.
Пусть сторона ромба х , ∠DCB=α , ВН⊥DC. Тогда углом между плоскостью (DC₁D₁) и прямой ВС₁ будет ∠ВНС₁=β .
ΔВНС-прямоугольный , ВН=х*sinα.
ΔBHC₁-прямоугольный , ВН=ВС₁*sinβ .
ΔBCC₁ прямоугольный ,BC₁=√(x²+a²), поэтому
ВН=√(x²+a²)*sinβ . Приравняем правые части для ВН и найдем сторону ромба.
х*sinα=√(x²+a²)*sinβ , х²*sin²α=(x²+a²)*sin²β , х²*sin²α-x²*sin²β=a²*sin²β , х²*(sin²α-sin²β)=a²*sin²β , х=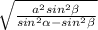
, x=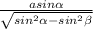
.
S(бок)=4а* 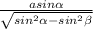, S(бок)=
.
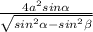V=а²sinα*а=а³sinα
==============
Угол между прямой и плоскостью .это угол между основанием перпендикуляра и основанием наклонной.
Пусть одна диагональ равна x, тогда другая (x+14)
S=d1*d2/2
120=x*(x+14)/2
x^2+14x-240=0
D=b^2-4ac=196+240=1156
x1=(-b+sqrt(D))/2a=(-14+34)/2=10
x2=(-b-sqrt(D))/2a=(-14-34)/2=-24 <0 – побочное решение
тогда диагонали равны 10 и (10+14)=24
Пусть сторона ромба равна a, тогда по теореме Пифагора
a^2=(d1/2)^2+(d2/2)^2
a^2=5^2+(12)^2=25+144=169
a=13
p=4a
p=4*13=52