Объяснение:
АВСД -прямоугольная трапеция ,ВС=4√2 , ∠А=45°, ∠Д=90°, АС-биссектриса ∠А.
1)Т.к АС-биссектриса, то ∠САД=∠САВ.
2)Т.к. АД║ВС ( основания трапеции), АС-секущая, то ∠ДАС=∠ВСА , как накрест лежащие. Значит в ΔАСВ есть два равных угла по 22,5° ⇒ ΔАСВ-равнобедренный и ВС=ВА=4√2.
3)Пусть ВК⊥АД, тогда ΔВКА-прямоугольный и равнобедренный , т.к. ∠КВА=90°-45°=45°. Обозначим равные катеты через х. По т. Пифагора :х²+х²=(4√2)², 2х²=16*2, х=4, КА=ВК=4.
3)Т.к. ВК⊥АД, то ДК=4√2.
4)ΔДВК-прямоугольный, по т. Пифагора ДВ²=КВ²+КД²,
ДВ²=16+16*2,
ДВ²=3*16
ДВ=4√3
15
Объяснение:
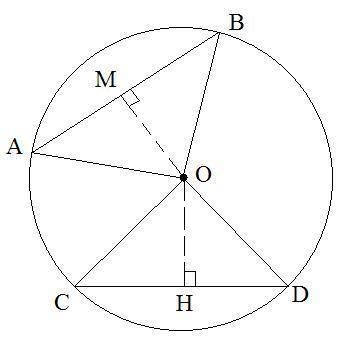
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15
хС = 0,5(хВ + хА) = 0,5(-2 + 4 ) = 1
уС = 0,5(уВ + уА) = 0,5(1 -3) = -1
ответ: С(1; -1)