Хорошо, давайте решим эту задачу. Для начала, мы знаем координаты точек e и f. Для нахождения длины отрезка ef, мы можем использовать формулу расстояния между двумя точками в декартовой системе координат.
Формула расстояния между двуми точками в декартовой системе координат:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Теперь подставим значения координат e и f в формулу расстояния:
E(-5;2) и F(7;-6)
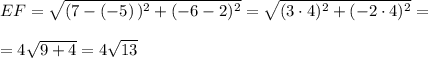
Формула координат середины M(x;y) отрезка с концами A(A₁;A₂) и B(B₁;B₂):Пусть M(x;y) середина EF.
ответ: EF = 4√13; M(1;-2).