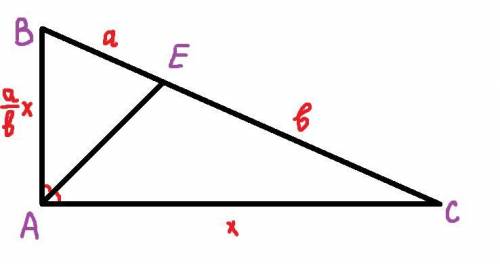
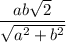Дан прямоугольный треугольник авс (угол с=90°) точка е принадлежит прямой ас, точка f прямой ав, ef||cb, ек - биссектриса треугольника aef. чему равен угол аек? , ! 7 класс

👇

Ответ:

tagirok4525

18.05.2023

Решение задачи во вложенном файле.
Дан прямоугольный треугольник авс (угол с=90°) точка е принадлежит прямой ас, точка f прямой ав, ef|

4,4(81 оценок)

Открыть все ответы

Ответ:

dragon64

18.05.2023

Пусть х см-одна сторона
(х+5)см-другая сторона прямоугольника
Р-2*(а+в); 2*(х+х+5)=50
2х+5=25
2х=25-5
2х=20
х=10

10см-одна сторона прямоугольника; 10+5=15(см)-другая
2. угол А-угол прямоугольника
3х+6х=90, где 3хград и6х град-углы, которые образует диагональ со сторонами прям-ка
9х=90; х=10; 3*10=30град; 6*10=60град
Сумма углов треуг-каАОВ 180град: 60+60+х=180; х=60град
Из треуг-каАОД 30+30+х=180; х=120
60град-угол между диагоналями (берём наименьший!)
3. АВСД-параллелограмм; ВД-диагональ, ВД перпендикуляна АД! ВД=АД
тр-ник АВД-прямоугольный; tgA=BD /AD; tgA=1; УголА=45град
уголС=углуА=45гра(противоположные углы парал-ма)
УголА+уголВ=180град; УголВ=180-45; уголВ=135град
уголД=углуВ=135град
ответ. 45град;135град;45; 135градусов

4,5(96 оценок)

Ответ:

овшаь

18.05.2023

Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

Запишем пропорцию:

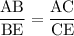
$\rm{\dfrac{AB}{BE}= \dfrac{AC}{CE}}$

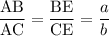
$\mathrm{\dfrac{AB}{AC}= \dfrac{BE}{CE}}=\dfrac{a}{b}$

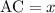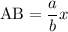Пусть $\mathrm{AC}=x$ . Тогда $\mathrm{AB}=\dfrac{a}{b} x$ .

Запишем теорему Пифагора для треугольника АВС:

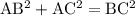
$\rm{AB^2+AC^2=BC^2}$

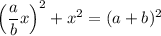
$\left(\dfrac{a}{b} x\right)^2+x^2=(a+b)^2$

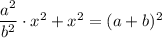
$\dfrac{a^2}{b^2}\cdot x^2+x^2=(a+b)^2$

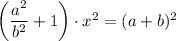
$\left(\dfrac{a^2}{b^2}+1\right)\cdot x^2=(a+b)^2$

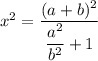
$x^2=\dfrac{(a+b)^2}{\dfrac{a^2}{b^2}+1}$

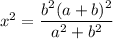
$x^2=\dfrac{b^2(a+b)^2}{a^2+b^2}$

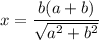
$x=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

Значит:

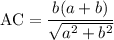
$\mathrm{AC}=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

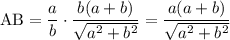
$\mathrm{AB}=\dfrac{a}{b}\cdot \dfrac{b(a+b)}{\sqrt{a^2+b^2} }=\dfrac{a(a+b)}{\sqrt{a^2+b^2} }$

Запишем теорему синусов для треугольника АЕС:

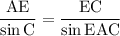
$\rm{\dfrac{AE}{\sin C} =\dfrac{EC}{\sin EAC} }$

Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.

Синус угла С определим как отношение противолежащего катета к гипотенузе:

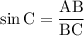
$\rm{\sin C=\dfrac{AB}{BC} }$

Теперь можем найти биссектрису:

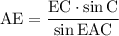
$\rm{AE =\dfrac{EC\cdot\sin C}{\sin EAC} }$

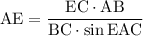
$\rm{AE =\dfrac{EC\cdot AB }{BC \cdot\sin EAC} }$

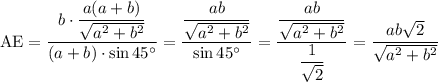
$\mathrm{AE} =\dfrac{b\cdot\dfrac{a(a+b)}{\sqrt{a^2+b^2} } }{(a+b) \cdot\sin 45^\circ}=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{ \sin 45^\circ} }=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{\dfrac{1}{\sqrt{2} } }=\dfrac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$