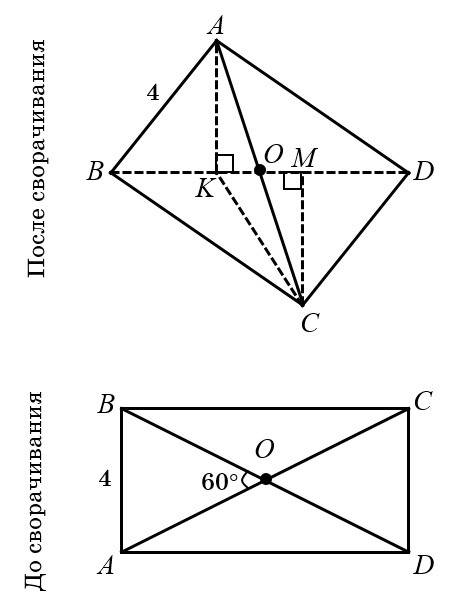
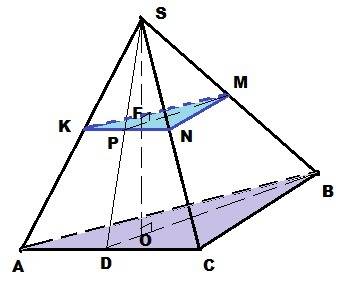
Дано: ABCD – прямоугольник, (ABD) ⊥ (CBD), AB = 4 см, ∠AOB = 60°
Найти: AC (после сгиба)
1) До сгиба:
ΔAOB – равносторонний АО = ВО = 4 см АС = BD = 2 × 4 = 8 см
2) После сгиба:
ΔBAD (∠BAD = 90°):
По теореме Пифагора: AD = √BD² – AB² = √8² – 4² = √64 – 16 = √48 = 4√3 см
AK = AB × AD / BD = 4 × 4√3 / 8 = 2√3 см = MC
ΔAKB (∠AKB = 90°):
По теореме Пифагора: BK = √AB² – AK² = √4² – (2√3)² = √16 – 12 = √4 = 2 см
BK = MD = 2 см
KM = BD – (BK + MD) = 8 – (2 + 2) = 4 см
ΔKMC (∠KMC = 90°):
По теореме Пифагора: KC = √KM² + MC² = √4² + (2√3)² = √16 + 12 = √28 = 2√7 см
ΔAKC (∠AKC = 90):
По теореме Пифагора: AC = √AK² + KC² = √(2√3)² + (2√7)² = √12 + 28 = √40 = 2√10 см
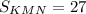 дм²
дм²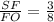
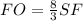
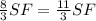
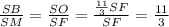
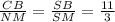 ⇒
⇒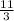
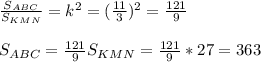
Уравнение окружности
(x+4)² + (y+6)² = 10²
Биссектриса c - прямая линия, наклонена под углом 45° к оси ОХ, проходит через начало координат.
Уравнение y = kx + b = tg 45°x + 0 = 1*x ⇒ y=x
Точки пресечения окружности (x+4)² + (y+6)² = 10² и прямой y=x
(x+4)² + (x+6)² = 10²
x² + 8x + 16 + x² + 12x + 36 = 100
2x² + 20x - 48 = 0
x² + 10x - 24 = 0
D/4 = 25 + 24 = 49 = 7²
x₁ = -5 + 7 = 2 y₁ = 2
x₂ = -5 - 7 = -12 y₂ = -12
Биссектриса a - прямая линия, наклонена под углом 135° к оси ОХ, проходит через начало координат.
Уравнение y = kx + b = tg 135°x + 0 = -1*x ⇒ y=-x
Точки пресечения окружности (x+4)² + (y+6)² = 10² и прямой y=-x
(x+4)² + (-x+6)² = 10²
x² + 8x + 16 + x² - 12x + 36 = 100
2x² - 4x - 48 = 0
x² - 2x - 24 = 0
D/4 = 1 + 24 = 25 = 5²
x₁ = 1 + 5 = 6 y₁ = -6
x₂ = 1 - 5 = -4 y₂ = 4
Точки пересечения окружности с биссектрисой 1 и 3 координатных четвертей A(2;2), B(-12;-12)
Точки пересечения окружности с биссектрисой 2 и 4 координатных четвертей D(6;-6), F(-4; 4)