Боковая сторона равнобедренного треугольника равна 10 см, а его основание 12 см. Найдите его площадь.
Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК и КС, равные соответственно 8 см и 4 см. Найдите периметр параллелограмма.
В трапеции ABCD углы А и В прямые. Диагональ АС — биссектриса угла А и равна 6 см. Найдите площадь трапеции, если угол CDA равен 60°.
В окружности проведены две хорды АВ и CD, пересекающиеся в точке К, КС = 6 см, АК = 8 см, ВК + DK = 16 см. Найдите длины ВК и DK.
Квадрат со стороной 8 см описан около окружности. Найдите площадь прямоугольного треугольника с острым углом 30°, вписанного в данную окружность.
Если боковые рёбра равны, то вершины проецируется в центр описанной окружности (Это следует из равенства 3 треугольников по общему катету-высота пирамиды и гипотенузе-боковому ребру пирамиды). Тогда боковое ребро можно найти по теореме пифагора, где ребро - гипотенуза, радиус описанной окружности и высота пирамиды - катеты.
Для треугольника: 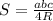
Где a,b,c - стороны; R-радиус описанной; S-площадь.
А площадь можно найти через формулу Герона.
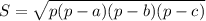
Где a,b,c-стороны треугольника; S-его площадь; p-полупериметр (половина от периметра).
А боковой ребро мы найдём: 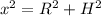
Где x-боковое ребро; R-радиус описанной; H-высота пирамиды.
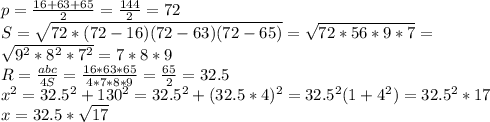
ответ: 32.5*√17.
Для ясности внизу рисунок.
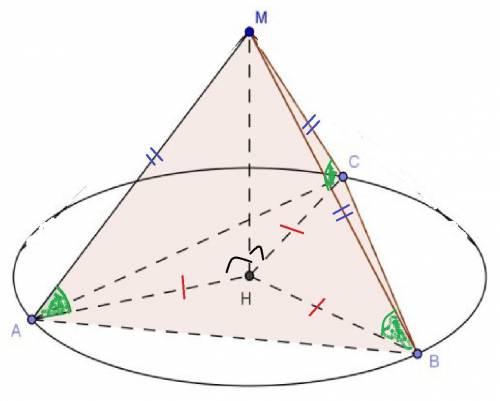
ABC-треугольник
AB=BC=CA
BH-высота
Pabc=42см
Найти AH
Решение:
*рисунок сделай сам*
1)AB=BC=AC => ABC- равносторонний.
Pabc=42 см
AB=BC=AC= Pabc/3
AB=BC=AC=42/3=14
2)ABC- равносторонний (т.к AB=BC=AC)
=>BH является медианой и высотой=> AH=1/2*AC
AH=1/2*14=7 см
ответ: AH=7 см