Правильная четырёхугольная пирамида 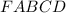 .
.
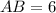 (см).
(см).
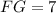 (см).
(см).
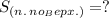 (см²).
(см²).
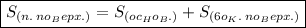
Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому 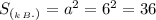 (см²).
(см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.Объяснение 1 правила: из этого следует, что апофема 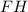 делит сторону основания
делит сторону основания 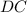 так, что
так, что 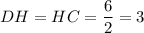 (см).
(см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный 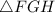 , где
, где 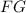 - катет прямоугольного тр-ка (высота пирамиды);
- катет прямоугольного тр-ка (высота пирамиды); 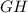 - катет прямоугольного тр-ка;
- катет прямоугольного тр-ка; 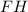 - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что
- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 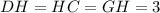 (см).
(см).
Так как апофема 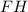 нашей пирамиды является ещё и гипотенузой прямоугольного
нашей пирамиды является ещё и гипотенузой прямоугольного 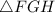 , то мы сможем найти её величину по т.Пифагора:
, то мы сможем найти её величину по т.Пифагора:
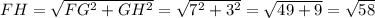 (см).
(см).
Теперь найдём периметр основания (квадрата):
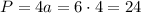 (см).
(см).
Затем найдём площадь боковой поверхности:
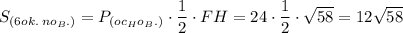 (см²).
(см²).
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
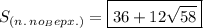 (см²).
(см²).
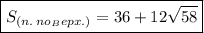 (см²).
(см²). 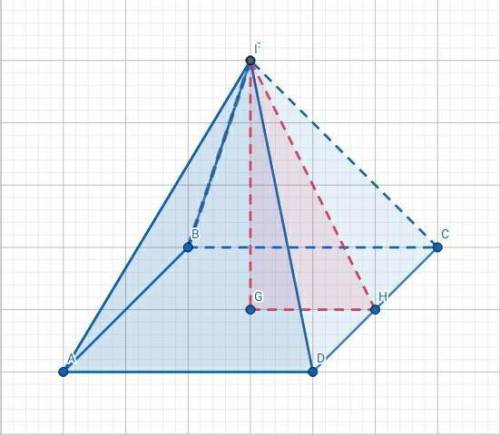
(x+3)² + (y+2)²=16
y = -x-1
(x+3)² + (-x-1+2)²=16
(x+3)² + (1-x)²=16
x² + 6x + 9 + 1 - 2x + x² = 16
2x² + 4x - 6=0
x² + 2x - 3 = 0
---
x₁ = (-2 - √(2² + 4*3))/2 = -1 -1/2*√16 = -1 - 2 = -3
y₁ = -x₁-1 = 3-1 = 2
(-3;2)
---
x₂ = (-2 + √(2² + 4*3))/2 = -1 + 1/2*√16 = -1 + 2 = 1
y₂ = -x₂-1 = -1-1 = -2
(1;-2)