По свойству (диагонали трапеции разбивают её на четыре треугольника с общей вершиной, площади треугольников, прилежащих к боковым сторонам, равны.) S(ABO)=S(CDO) , обозначим эту площадь S0 (действительно, S (ABD) = S(ACD) , т. к. у них общие основания и равные высоты, т. е. S(AOB)+S(AOD)=S(COD)+S(AOD) откуда следует S(AOB) =S(COD)).
Так как S(ABC)= S0+ S1= h*a/2 и S(ACD)= S0+ S2= h*b/2 , то (S0+S1)/(S0+S2)=a/b
Далее, треугольники BOC и DOA подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит S1/S2=(a/b)^2
Таким образом, (S0+S1)/(S0+S2) =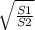 
Отсюда находим S1=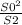 
=36/9=4
Поэтому площадь трапеции будет равна s= S1+S2+2S0= 4+9+12=25
ответ:Краткие решения:
1) AB = CD (св-во параллелограмма), ∠A = ∠B = ∠C = ∠D = 90° (определение прямоугольника). ∠ABN = ∠MCD = 45° (половины углов 90°). Значит, треугольники ABN, MCD – прямоугольные равнобедренные с равными катетами, поэтому эти треугольники равны и BN = CM
2) ∠B = 90°, из треугольника ABC: ∠ACB = 180° - 90° - 55° = 35°. BO = OC (св-во прямоугольника), значит, ∠CBO = ∠ACB = 35°, ∠COD = ∠CBO + ∠ACB = 70° (внешний угол к треугольнику BOC).
3) AO = OB, ∠OAB = ∠OCD = 60° (накрест лежащие углы), тогда треугольник AOB – равносторонний, BE – медиана. AO = 2OE = 8 (определение медианы), AC = 2AO = 16 (св-во параллелограмма).
4) ∠A = ∠B = ∠C = ∠D, тогда 4 маленьких треугольника равны по двум сторонам и углу между ними, откуда A₁B₁ = B₁C₁ = C₁D₁ = D₁A₁, A₁B₁C₁D₁ – ромб.