Точки K, E, N , F середины сторон AB,BC,CD и DA выпуклого четырехугольника ABCD. известно что AC=BD=30 см. найдите периметр четырехугольника KENF
Объяснение:
ΔАВС , КЕ-средняя линия , тк по условию точки K, E-середины сторон AB,BC. По т. о средней линии КЕ=1/2*АС=1/2*30=15 (см).
ΔАDС , NF-средняя линия , тк по условию точки N,F-середины сторон CD,DA. По т. о средней линии NF=1/2*АС=1/2*30=15 (см)
ΔАВD , КF-средняя линия , тк по условию точки K, F-середины сторон AB,AD. По т. о средней линии КF=1/2*BD=1/2*30=15 (см)
ΔВСD , EN-средняя линия , тк по условию точки E, N-середины сторон BC,CD. По т. о средней линии ЕN=1/2*BD=1/2*30=15 (см)
P=4*15=60 *см).
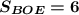
Объяснение:
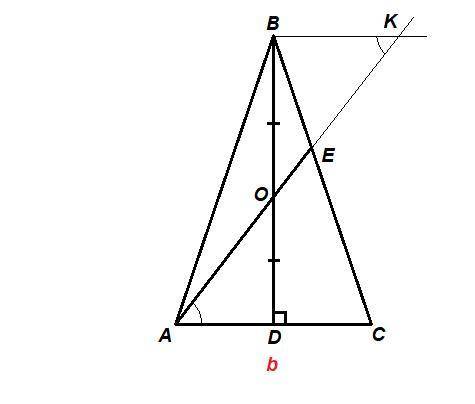
Проведем ВК║АС (К - точка пересечения прямых ВК и АЕ).
ΔВОК = ΔDOA по стороне и двум прилежащим к ней углам (ВО = OD, ∠ВКО = ∠DAO как накрест лежащие при ВК║АС и секущей АК, углы при вершине О равны как вертикальные), ⇒
ВК = AD = b/2
ΔBKE ~ ΔCAE по двум углам (∠ВКО = ∠DAO, углы при вершине Е равны как вертикальные),
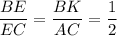
Площади треугольников с общей высотой относятся как стороны, к которым можно провести эту высоту.
В треугольниках АВЕ и АСЕ можно провести общую высоту из вершины А к сторонам ВЕ и ЕС соответственно, поэтому
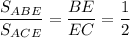
То есть
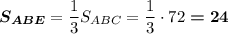
BD - медиана равнобедренного треугольника АВС, делит его на два равновеликих:

AO - медиана треугольника ABD, делит его на два равновеликих:
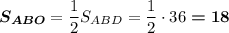
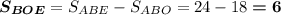
AB не ∩ α, AO=OB
AA₁_|_α, BB₁_|_α, OO₁_|_α
A₁∈α, B₁∈α , O₁∈α .
AA₁=7,4 см, BB₁=6,1 см
найти: ОО₁
решение.
AA₁_|_ α, BB₁_|_ α , => AA₁ || BB₁
AA₁B₁B - трапеция
OO₁ - средняя линия трапеции
OO₁=6,75 см