DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.
8+16√2 см²
Объяснение:
Дано:
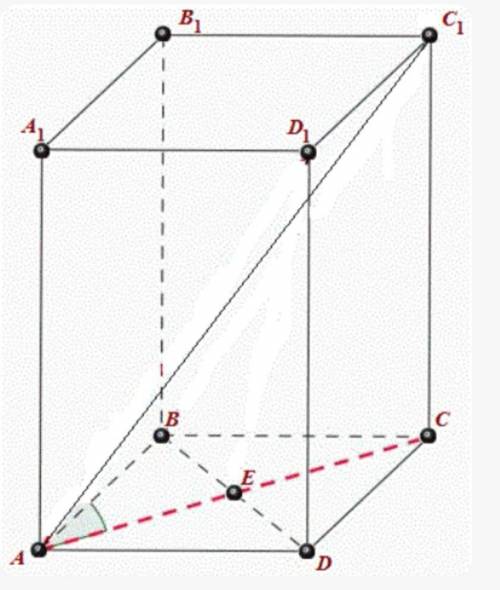
АВСDA1B1C1D1 призма.
АВСD- квадрат.
АС1=4см диагональ призмы.
АВ=ВС=СD=AD=2см
Sпол=?
Решение
Sпол=2Sосн+Sбок
Sосн=АВ²=2²=4 см² площадь квадрата.
АС- диагональ квадрата.
АС=АВ√2=2√2 см диагональ квадрата.
∆АС1С- прямоугольный.
АС1- гипотенуза.
АС и СС1 - катеты.
По теореме Пифагора найдем СС1
СС1=√(АС1²-АС²)=√(4²-(2√2)²)=√(16-8)=√8=
=2√2 см высота призмы.
Формула нахождения площади боковой поверхности призмы
Sбок=Росн.*h, где Росн.-периметр основания (квадрата); h=CC1.
Sбок=4*АВ*СС1=4*2*2√2=16√2 см² площадь боковой поверхности призмы.
Sпол.=2*Sосн.+Sбок=2*4+16√2=8+16√2 см² площадь полной поверхности призмы.
{x>2,5 (2,5)
⇒ x>2,5 или x∈(2,5 ; +∞)