АВ=13; EF=8
Объяснение:
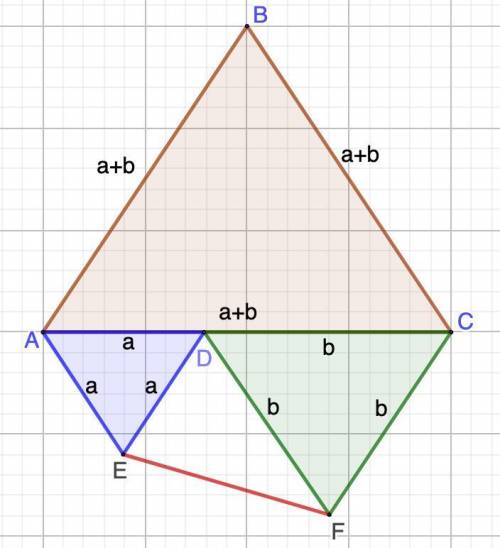
Дано: ΔАВС - равносторонний;
Δ ADE и ΔDCF - равносторонние
Р (ΔDEF) = 21
P (ABCFE) = 47
Найти: АВ; EF
Треугольники равносторонние ⇒ у них все стороны равны.
Пусть сторона ΔAED равна a, а сторона ΔDCF равна b.
⇒ сторона ΔАВС равна a+b.
1. Рассмотрим ΔEDF.
P (ΔEDF) = 21 ⇒ EF =21 - (a+b) = 21 - a - b
2. Рассмотрим ABCFE.
Р (ABCFE) = 47
Периметр - сумма длин всех сторон.Р (ABCFE) = AB + BC + CF + EF +AE
47 = a+b+a+b+b+21-a-b+a
47 = 2a +2b +21
2(a+b) = 26
a+b = 13
3. АВ = a+b = 13
EF = 21 - (a+b) = 21 -13 = 8
6х+х+11х=180
18х=180
х=10
Угол А=10*6=60 градусов (другие углы находить не обязательно).
По теореме косинусов найдем ВС:
ВС²=АВ²+АС²-2*АВ*АС*cos60=25+121-2*5*11*0,5=91
ВС=√91≈9,5 (ед.)
ответ: 9,5 ед.