Здравствуй qwertyvv!
В треугольнике ABC угол В в 4 раза меньше угла А, а угол С на 60° больше угла В. Найдите углы B, А, С.
Для начала напишем известные нам условия, и так
Дано:
ΔABC
∠B < ∠A в 4 раза
∠C > B на 60°
Найти:
А, В, С
Данную задачу мы будем решать через уравнение.
Пусть ∠B - х°, а угол А - 4х, тогда угол C = х+60. Зная, что сумма всех углов в треугольнике равняется 180°. Составим и решим уравнение:
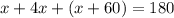
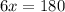
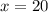
Значит, ∠В = 20°, тогда угол С= 20+60=80, а ∠А = 20 * 4 = 80
ответ: ∠В = 20°; ∠С = 80°; ∠А = 80°
Удачи в последующих решениях!
проекция длинной боковой стороны на основание 20-b см
высота 9 см
По Пифагору
9² + (20-b)² = 15²
81 + (20-b)² = 225
(20-b)² = 225 - 81 = 144 = 12²
20-b₁ = 12
b₁ = 8 см
20-b₂ = -12
b₂ = 32 см - много, больше основания, отбросим это решение, оно соответствует невыпуклой фигуре
итак, b = 8 см
И средняя линия
l = 1/2(a+b) = 1/2(8+20) = 14 см