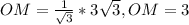
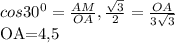
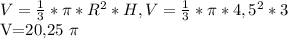
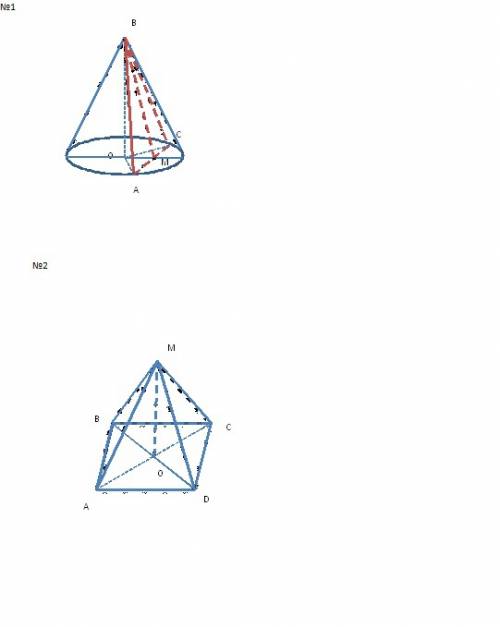
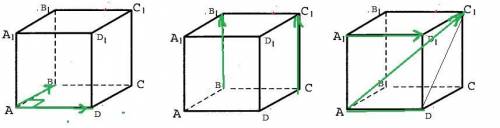
В кубе ABCDA1B1C1D1 найдите угол между векторами:
a)AB и AD , б)BB1 и CC1 , в)AC1 и A1D1
Объяснение:
Углы между векторами а)∠АВ,АD=90°, т.к все грани куба являются квадратами.
б) ∠ВВ₁,СС₁=0°, т.к эти вектора лежат на параллельных прямых.
в) ∠АС₁,А₁D₁=arcctg√2.
Т.к. вектор А₁D₁=AD , то найдем угол ∠АС₁,АD
Из ΔВСС₁ -прямоугольный. Пусть ребро куба а, тогда по т. Пифагора
ВС₁=а√2.
По т. о трех перпендикулярах если проекция ВС перпендикулярна , прямой лежащей в плоскости АВ, то и наклонная С₁В перпендикулярна прямой лежащей в плоскости АВ⇒ ΔАВС₁-прямоугольный .
tg∠С₁FD=BС₁/AB или tg∠С₁FD=а√2/а , tg∠С₁FD=√2 , ∠С₁FD=arctg√2,
а значит у угол между векторами ∠АС₁,А₁D₁=arcctg√2.
Второй угол возьмем за х
Первый угол в таком случае х-30
А третий - (х-30)/7
Зная, что сумма всех углов треугольника=180 градусов, составим уравнение:
х+(х-30)+((х-30)/7)=180
х+х-30+0,143x-4,29=180
2,143x=214,29
x=214,29/2,143
x=99,99~100
Тогда 1ый угол=100-30=70
И третий=70/7=10
ответ: первый угол=70 градусов, второй 100, третий 10.