Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png) с одной стороны и
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png) с другой.
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
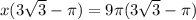
площадь круга = 9Пи
Найдем радиус круга
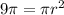
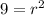
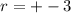
Т к радиус не может быть отрицательным то он равен 3
Площадь прав тр через радиус вписанной окружности равен 3 корня из 3 на радиус в квадрате, а площадь вписанного круга равна Пи на радиус в квадрате.
Рассмотрим во сколько раз площадь треугольника больше площади круга. ![\frac{3 \sqrt[]{3}r^{2}}{\pi r^{2}}=\frac{3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/07e0a.png)
Пусть площадь круга х, тогда площадь треугольника (по условию) ![x+27\sqrt[]{3}-9\pi](/tpl/images/0144/4450/08b8d.png) с одной стороны и
с одной стороны и ![\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/56410.png) с другой.
с другой.
Получим уравнение ![x+27\sqrt[]{3}-9\pi=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/99a9d.png)
Разрешим относительно х. Приведем к знаменателю Пи и приравняем числители
![\frac{x\pi}{\pi}+\frac{\pi27\sqrt[]{3}}{\pi}-\frac{9\pi^{2}}{\pi}=\frac{x3 \sqrt[]{3}}{\pi}](/tpl/images/0144/4450/4f04e.png)
![x\pi}+\pi27\sqrt[]{3}-9\pi^{2}=x3 \sqrt[]{3}](/tpl/images/0144/4450/57c86.png)
Вынесем 3 корня из трех - Пи за скобки и получим
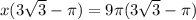
площадь круга = 9Пи
Найдем радиус круга
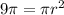
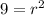
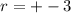
Т к радиус не может быть отрицательным то он равен 3
Ох, боюсь, опять меня накажут :)))
радиус шара 1, поэтому вертикальное сечение конуса - треугольник имеет высоту 3, и центр вписанной в него окружности совпадает с точкой пересечения медиан. Отсюда сразу следует, что треугольник равносторонний. : (на самом деле - это ОЧЕНЬ строгое доказательство, но - из разряда "не для чайников". Точка пересечения биссектрисс и медиан - одна и та же точка.)
Поэтому у конуса радиус основания равен корню из 3, а объем - 3пи мое решение НЕ ОТМЕЧАТЬ :)))