Найдите:
так как тругольник АВС равносторонний все стороны равны а и углы равны 60 град
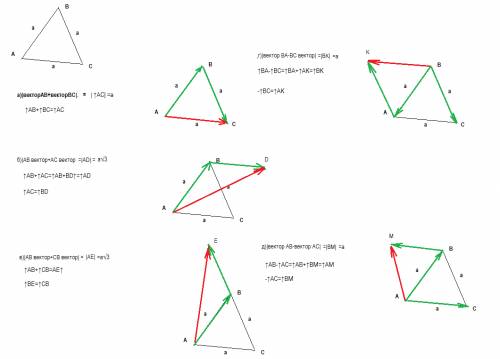
а)|векторAB+векторBC|=|векторAC|= а
б)|AB вектор+АС вектор|=|AD|=a√3
при параллельном перносе вектора АС получается вектор ВД
сумма векторов АВ и ВД -вектор АД
в треугольнике АВД угол В=120 град
по теореме косинусов
АД^2 = AB^2+BD^2 -2 AB*BD*cos 120= a^2+a^2-2aa*(-1/2)=2a^2+a^2=3a^2
AD = a√3
в)|AB вектор+CB вектор|=|AE|=a√3
при параллельном перeносе вектора СB получается вектор ВE
сумма векторов АВ и ВE =вектор АE
в треугольнике АВE угол AВE=120 град
по теореме косинусов
АE^2 = AB^2+BE^2 -2 AB*BE*cos 120= a^2+a^2-2aa*(-1/2)=2a^2+a^2=3a^2
AE = a√3
г)|вектор ВА-ВС вектор|=|BK|= а
при параллельном перeносе вектора -BC получается вектор ВK
сумма векторов ВA и AK =вектор BK
трекгольник ABK - равносторонний все стороны равны ВК=а
д)|вектор АВ-вектор AC|=|вектор АВ+вектор ВМ|=|AM|=a
в раностороннем треугольнике АВМ - все стороны равны а --АМ=а
1)Пусть х-одна часть, тогда боковая сторона-5х, а основание-2х, по условию 5х+5х+2х=60
решим уравнение
12х=60
х=5- это одна часть, значит боковая сторона = 25, а основание=10
2)Дополнительно построем из вершины лежащей против основания высоту, которая будет и медианой (по свойству равнобедренного треугольника)
Тогда полученный отрезок основания будет равен 5
Получим прямоугольный треугольник с гипотенузой равной 25 и катетом равным 5, по теореме Пифагора находим второй катет (теорема Пифагора-c^2=a^2+b^2 где с гипотенуза а остальное катеты)
значит составим уравнение
25 во 2 степени=5 во второй степени + высота которую мы дополнительно построили
отсюда следует что высота равна 10 корням из 6
3)Площадь треугольника=1/2 основания на высоту
основание найдено в пункте 1, оно равно 10 высота равна 10 корней из 6
площадь равна 50 корням из 6
ответ: S=50 корней из 6
P.S. Знака корня нет на клаве, писал словами))