ответ: Sосн=225π(см²);
Sбок.пов=375π(см²); Sпол=600π(см²);
V=1500π(см³); Sсеч=300см²
Объяснение: образующая конуса с радиусом образуют прямоугольный треугольник, в котором радиус и высота - катеты, а образующая- гипотенуза. Найдём высоту конуса h по теореме Пифагора:
h²=обр²-r²=25²-15²=625-225=400;
h=√400=20см
Так как осевым сечением конуса является треугольник, то его площадь вычисляется по формуле:
S=½×а×h, где а- сторона треугольника, а h- высота проведённая к стороне. Стороной бокового сечения является диаметр конуса=15×2=30см
Sсеч=½×30×20=15×20=300см²
Найдём площадь основания по формуле:
S=πr², где r- радиус основания:
Sосн=π×15²=225π(см²)
Площадь боковой поверхности конуса вычисляется по формуле: S=πrl, где r=радиус, а l- образующая:
Sбок.пов=π×15×25=375π(см²)
Чтобы найти полную площадь поверхности конуса нужно суммировать обе площади: основания и боковой поверхности:
Sпол=Sбок.пов+Sосн=
=375π+225π=600π(см²)
Теперь найдём объем конуса по формуле: V=⅓×Sосн×h=225π×20=4500π×⅓=
=1500π(см³)
Правильная четырёхугольная пирамида.
Стороны оснований = 5 см, 17 см.
Найти:А1С - ?
Решение:"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".
Так как данная пирамида - правильная, четырёхугольная => основание данной пирамиды - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
НО: Заметим, что нам даны совершенно разные величины оснований пирамиды.
=> перед нами - усечённая правильная четырёхугольная пирамида.
"Усечённая пирамида - часть пирамиды, заключённая между её основанием, боковыми гранями и сечением этой пирамиды".
=> CD = 17 (см), А1В1 = 5 (см).
Итак, у нас два квадрата А1В1С1D1 и АВСD, которые являются основаниями этой усечённый пирамиды.
Диагональным сечение данной усечённой пирамиды является равнобедренная трапеция А1АС1С.
Проведём высоту А1К.
Так как А1С1 и АС - диагонали квадратов АВСD и A1B1C1D1 => A1C1 = A1B1 * √2 = 5 * √2 = 5√2 (см)
Также АС = CD * √2 = 17√2 (см).
А1К ┴ АС, С1Н ┴ АС, так как А1К и С1Н - высоты.
=> А1С1НК - прямоугольник. => А1С1 = КН, А1К = С1Н.
Рассмотрим △АА1К и △СС1Н:
А1К = С1Н, так как А1С1НК - прямоугольник.
АА1 = С1С, так как А1АС1С - равнобедренная трапеция.
=> △АА1К = △СС1Н, по карету и гипотенузе.
=> АК = СН = 1/2(АС - А1С1) = 1/2(17√2 - 5√2) = 6√2 (см)
=> СК = АС - АК = 17√2 - 6√2 = 11√2 (см)
Найдём А1С, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
√(4² + (11√2)²) = √(16 + 121 * 2) = √258 (см)
ответ: √258 (см)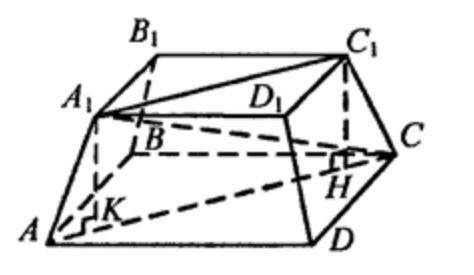
угол ВАМ=90/2=45 ( бисс-са делит угол пополам) угол АМВ=90 (т.к в равнобедр треуг-ке биссек-са является высотой)