Виды треугольников :
по размерам сторон :
разносторонние (треугольник, все стороны которого имеют разную длину.)
равнобедренные (это треугольник, у которого две стороны равны.)
равносторонние (это треугольник, у которого все три стороны равны.)
по размерам углов:
прямоугольные - это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
остроугольные- это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º)
тупоугольные - это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Средняя линия треугольника-это отрезок,соединяющий серидины сторон треугольника.
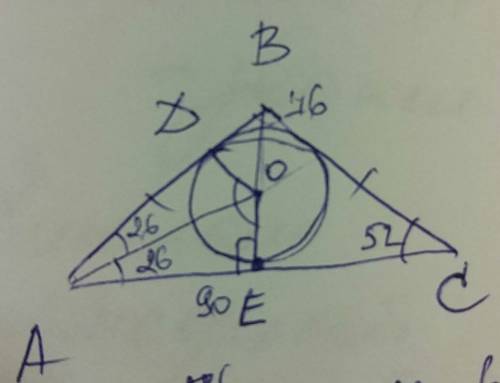
В прямоугольном треугольнике АВС: <A+<DCB=90° (сумма острых углов прямоугольного треугольника).
Тогда и <A+<DBC=90° (1).
<В=<DBC+<ABD=90° (2) (так как <В=90° - дано). Значит
<A=<ABD - из (1) и (2). Тогда
треугольник АВD - равнобедренный и АD=ВD, что и требовалось доказать.