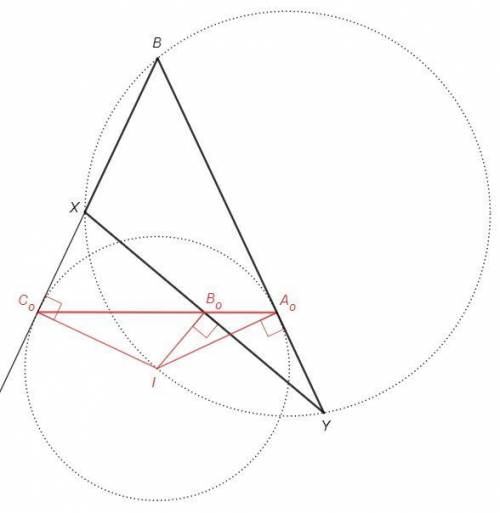
Из точки описанной окружности на прямые сторон треугольника опущены перпендикуляры. Основания перпендикуляров лежат на прямой Симсона.
Точка I лежит на биссектрисе угла B, следовательно делит дугу XY пополам. Пусть Bo - середина хорды XY. Тогда IBo - серединный перпендикуляр к XY (хорды IX и IY равны, стягивают равные дуги).
I - точка на окружности, описанной около треугольника XBY. IAo, IBo, ICo - перпендикуляры, опущенные на стороны треугольника XBY. Основания перпендикуляров Ao, Bo, Co лежат на прямой Симсона.
1. АВ = 4см, ВС = 12 см, СD = 4см, АD = 12см
2. АС = 10см, ВС = 4см, АВ = 4см
Объяснение:
1. Одна сторона – х, другая – 3х. В параллелограмме стороны попарно равны и параллельны. Значит, Р=х + х + 3х + 3х = 8х = 32см. Получаем уравнение: 8х = 32. Из этого уравнения следует, что х = 32:8, х = 4см (мы нашли первую сторону). Вторая сторона: 4×3 = 12см.
2. Средняя линия в равнобедренном треугольнике равна половине основания и параллельна ему. Значит, АС = 2×DE = 2×5 = 10см. В равнобедренном треугольнике боковые стороны равны: АВ = ВС. Значит, мы можем периметр записать так: Р = 2×АВ + АС = 2×АВ + 10 = 18. Пусть АВ = ВС = х, мы получили уравнение: 2×х + 10 = 18
2×х = 18 - 10 = 8
х = 8:2 = 4, то есть АВ = 4см, ВС = 4 см
So=81, h=9 (куб).
V=(1/3)*81*9=243.
2. Sabc=(1/2)*AH*BC=60
Sbdc=(1/2)*DH*BC=40.
DH=(2/3)AH, DO=8.
Надо найти АР (перпендикуляр к DH)
Sadh=(1/2)*AH*8=4AH.
Sadh=(1/2)*AP*DH => AP=2Sadh/DH = 8AH/(2/3)AH = 12.