Відповідь: 2π см або 6,28 см
Пояснення:
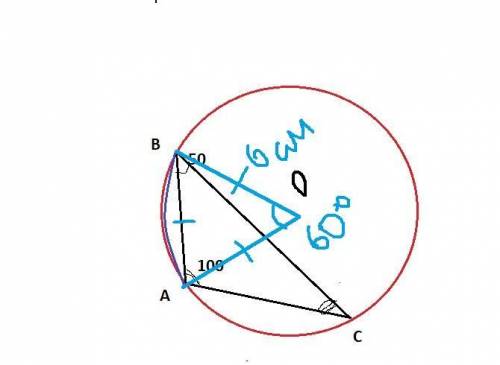
Дано :ΔАВС, АВ=6 см, ∠А=100°, ∠В=50°
Знайти: ∪АВ-?
Рішення:
Проти меншого кута лежить менша сторона, отже менший кут спираєтьсяна найменшу дугу.
За теоремою про суму кутів трикутника
∠А+∠В+∠С=180°
100°+50°+∠С=180°
∠С=180°-150°
∠С=30°
Отже ∪АВ- найменша, а ∠С- вписаний кут.
∠ АОВ- центральний- він = 60° (Вписаний кут дорівнює половині центрального кута)∠С=1/2 ∠АОВ → ∠АОВ=2∠С=2*30°=60°
Розглянемо ΔАОВ, де АО=ОВ= r , ∠АОВ=60°, так як кути при основі рівнобедреного трикутника рівні, то ∠ВАО=∠АВО
2∠ВАО+∠АОВ=180°( за теоремою про суму кутів Δ)
∠ВАО=∠АВО =(180-°60°):2=60°.
Всі кути рівні, отже ΔАОВ- рівносторонній АО=ОВ=АВ=r=6 cм
довжина дуги:
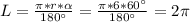 (cм)≈2*3,14≈6,28 см
(cм)≈2*3,14≈6,28 см
Объяснение:
Пусть с точки С опустили две наклонние на плоскость, в пересечении получили точки А и в
В результате имеем ДАВС, где /_С=90°
Опустим перпендикуляр с точки с на плоскость, получим точку Н Известно, что /_CAH=45° и /_СВН=30°, СВ=
Тогда из ДСНB /_H=90°, /_B=30°и CB=8 имеем
СН=4, как катет против угла 30°
Из ДСНА, где /_H=90° и /_A=45° следует, что и /_НСА=45° → ДСНА равнобедренний CH=HA=4
По теореме Пифагора СА=4√2
Из ∆АВС: /_C=90°, из условия, СВ=8,
CA=4√2
За теоремою Пифагора
ВА^2=СВ^2+СА^2=64+32=96
BA=4√6
Напомню теорему о том, что величина внешнего угла треугольника равна сумме двух внутренних его углов, не смежных с ним.
Именно поэтому внешний угол при вершине В равен сумме двух внутренних углов:
123° = ∠А + ∠С,
123° = 24° + ∠С,
∠С = 123° - 24° = 99°.
ответ: ∠С = 99°.