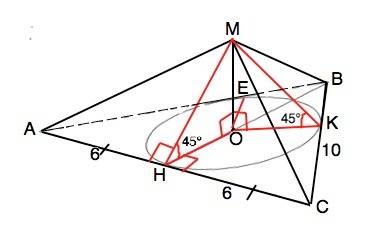
Если все грани пирамиды наклонены к плоскости основания под одним углом, то проекции высот этих граней равны радиусу вписанной в основание пирамиды окружности
ОН=ОК=ОЕ=r и, следовательно, высоты всех боковых граней равны.
r=2S (ABC):P
P=12+2•10=32
S=BH•AC:2=8•12:2=48 см²
2Ѕ=96 см²
∆ ABC - равнобедренный, его высота - медиана.
АН=СН=6 см
По т.Пифагора высота равнобедренного треугольника
ВH=√(ВС²-СН²)=√(100-36)=8 см
r=8•12:32=3 см
ВН⊥АС,
МН по т. о 3-х перпендикулярах перпендикулярен АС и является высотой боковой грани МАС.
МК=МН.
Из прямоугольного ∆ МОН отрезок МН=ОН:cosМНО=3:√2/2=3√2
S(бок)=МН•Р:2=48√2
S (полн)=Ѕ (АВС)+Ѕ(бок)=48+48√2=48(1+√2) см²
АВСД-равнобедренная трапеция с основаниями АД и ВС.
Опустим высоты ВН и СМ.
1)Найдём АН
АН=(АД-НМ):2=(АД-ВС):2=(49-15):2=17 (см)
2)В треугольнике АНВ угол Н=90 град, т.к. ВН-высота, угол А=60 град (по условию),
следовательно угол В=30 град. Это значит, что мы можем найти сторону АВ по следующему свойству: "В прямоугольном треугольнике против угла в 30 град лежит сторона равная половине гипотенузы", т.е. гипотенуза АВ=2*АН=2*17=34 (см)
3)Периметр трапеции Р=АД+АВ+ВС+СД=49+34+15+34=132(см)
ответ: 132 см
с=27; ∠А = 24°; ∠С = 90°. найти: а; b; ∠В
Решение:
SinA = a/c, ⇒ a = cSinA = 27*0,45 ≈12
∠B = 90° -27° = 63°
SinB = b/с, ⇒ b = cSinB = 27*0,89 ≈24