ответ: 18
Объяснение:
Параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.
1. Плоскости граней AA₁D₁D и ВВ₁С₁С параллельны. Они пересечены плоскостью (АВ₁С₁), значит линии пересечения параллельны.
(АВ₁С₁) ∩ (ВВ₁С₁) = В₁С₁,
В₁С₁ ║ВС и ВС║AD как противолежащие стороны прямоугольников, ⇒ В₁С₁ ║ AD. Тогда
(АВ₁С₁) ∩ (АА₁D₁) = AD.
AB₁C₁D - сечение параллелепипеда плоскостью (АВ₁С₁).
2. Секущая плоскость и плоскость (АВ₁С₁) параллельны, значит они пересекаются плоскостями граней параллелепипеда по параллельным прямым.
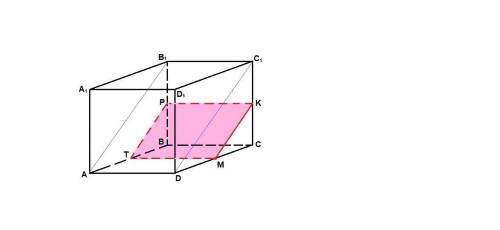
Проведем МТ║AD, MK║DC₁, TP║AB₁ и PK║B₁C₁.
MKPT - искомое сечение.
3. ТМ║ВС, ВТ║СМ, ∠ТВС = 90°, значит ТВСМ прямоугольник,
ТМ = ВС = 4.
Аналогично, РК = ВС = 4.
МКРТ - параллелограмм, так как МТ║РК и МТ = РК.
М - середина CD, МК║DC₁, значит МК - средняя линия ΔDCC₁, тогда К - середина СС₁.
ΔМКС: ∠МСК = 90°, МС = CD/2 = 4, СК = СС₁/2 = 3, значит МК = 5 (египетский треугольник).
Pmkpt = 2(TM + MK) = 2 · (4 + 5) = 2 · 9 = 18
Так как в равнобедренном треугольнике может быть только один тупой угол, значит, нужно найти углы при основании
(180° - 104°) : 2 = 76° : 2 = 38°
Два угла при основании равны по 38°
A2.
a) ∠С = 90°; ∠D = 30°
∠E = 90° - ∠D = 90° - 30° = 60°
EF - биссектриса ⇒ ∠DEF = 1/2 ∠E = 1/2 * 60° = 30°
ΔDEF : ∠DEF = ∠D = 30° ⇒ ΔDEF - равнобедренный
б) Биссектриса угла треугольника делит противолежащую сторону пропорционально прилежащим сторонам.
Так как катет CE меньше гипотенузы DE, значит, CF меньше DF:
CF < DF
A3. P = 77 см. Так как треугольник тупоугольный равнобедренный, то самая длинная сторона - основание ⇒
Пусть боковая сторона равна X см,
тогда основание равно Х + 17 см
Р = Х + Х + Х + 17 = 77
3X + 17 = 77
3X = 60
X = 20 см
X + 17 = 37 см
Стороны треугольника 20 см, 20 см, 37 см