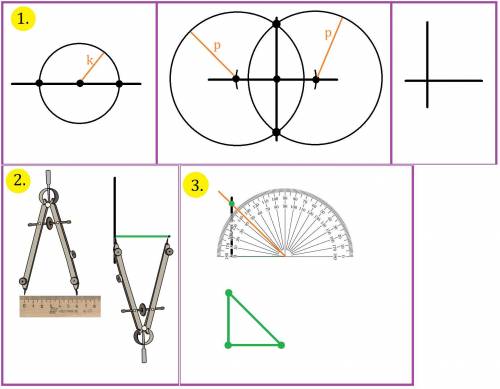
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.

Из ΔABP(в нем известны все стороны) найду cosB по т. косинусов
AP^2=AB^2+BP^2-2*AB*AP*cosB
5^2=6^2+3^2-2*6*3*cosB
25=45-36cosB
cosB=20/36=5/9
Теперь найду АС по этой же теореме
AC^2=6^2+6^2-2*6*6*5/9
AC^2=72-40=32
AC=4√2
AH1=AC/2=2√2
BH1^2=AB^2-AH1^2=6^2-(2√2)^2=36-8=28
AH=2√7
ΔABH1 и ΔACH подобны по 2 углам
AB/AC=BH1/AH
6/(4√2)=2√7/AH
AH=4√14/3
сos<PAH=AH/AP=4√14/(3*5)=4√14/15≈0.99