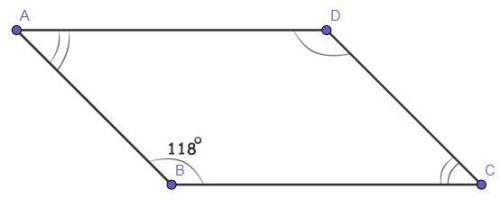
Четырёхугольник ABCD - параллелограмм.
∠В - тупой.
∠В = 118°.
Найти :Острый угол параллелограмма = ?
Решение :Если в параллелограмме имеется один тупой угол, то в этом параллелограмме есть ещё один тупой угол и два острых угла.Нам дан один тупой угол - это ∠В. А как теперь понять какой ещё тупой угол в этом параллелограмме?
А дело в том, что -
В параллелограмме противоположные углы равны.На рисунке ∠В = ∠D = 118°.
Тогда остаётся, что ∠А = ∠С - острые.
Сумма внутренних углов любого четырёхугольника равна 360°.То есть -
∠А + ∠В + ∠С + ∠D = 360°
∠А + ∠C = 360° - ∠В - ∠D
∠А + ∠C = 360° - 118° - 118°
∠А + ∠C = 124°
∠A = ∠C = 124° : 2 = 62°.
ответ :62°.
Зеленим кольором позначив площину.
Оскільки призма ПРАВИЛЬНА то BB1⊥ (ABC), тому (ABC)⊥(BB1C1) за ознакою перпендикулярності площин.т.A∈(ABC), тому за властивістю перпендикулярних площин р(A;(BB1C1)) , AK=d, бо AK⊥BC, як медіана і висота рівностор. трикутника.
B1K- похила, BK- проекція на (ABC), BK⊥AK, бо BC⊥AC, тому за ТТП B1K⊥AK, AK-лінія перетину (ABC)∩(AB1K). Тоді за означенням кута між площинами ∠B1KB=a.
Vпризми-?
Vпр=S(основи)*h=S(abc)*BB1=
BC-? BB1-?
Відомо, що AK=BC√3/2. d=BC√3/2⇒BC√3=2d⇒2d/√3
ЗΔB1BK (∠BB1K=90°) BB1=BK*tgB1KB⇒BB1=1/2BC*tga⇒B1B=1/2*2d/√3*tg(a)=tg(a)/√3
Отже V призми=(2d/√3)²√3*d√3*tg(a)/4*√3=
Відповідь: