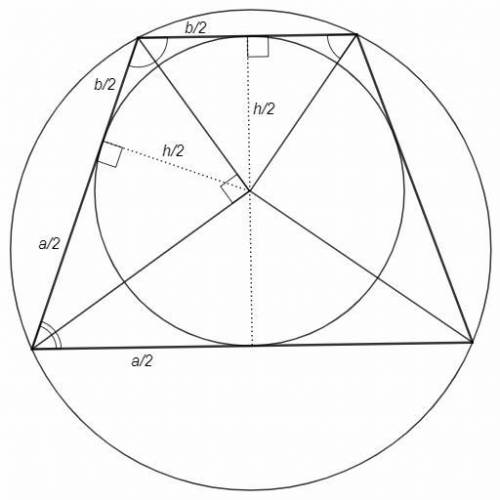
Трапеция описанная, следовательно её биссектрисы пересекаются в одной точке (центр вписанной окружности). Трапеция вписанная, следовательно равнобедренная, углы при основании равны. Значит равны их половины, биссектрисы углов при основании образуют равнобедренный треугольник. Перпендикуляр из центра вписанной окружности к основанию (радиус) является медианой.
Биссектрисы внутренних углов при параллельных пересекаются под прямым углом. Радиус в точку касания на боковой стороне - высота из прямого угла, она равна среднему пропорциональному проекций катетов. Отрезки касательных из одной точки равны, проекции катетов равны половинам оснований. Радиус равен половине высоты. Таким образом h=√(ab)
24см;МА=7см;МА перпендикулярно (АВСД)
∆МАВ МВ²=МА²+АВ²=24²+7²=576+49= 625=
=25²;МВ=25;МВ=МД=25
площадь ∆МАВ=24•7/2=12•7=84(см квадрат)
площадь∆МАД=84(см квадрат)
по ТТП <МДС=90°
площадь ∆МДС=
24•25/2=12•25=300(см квадрат)
площадь боковой
поверхности
2•84+2•300=768см квадрат